深度学习
神经网络
整体框架
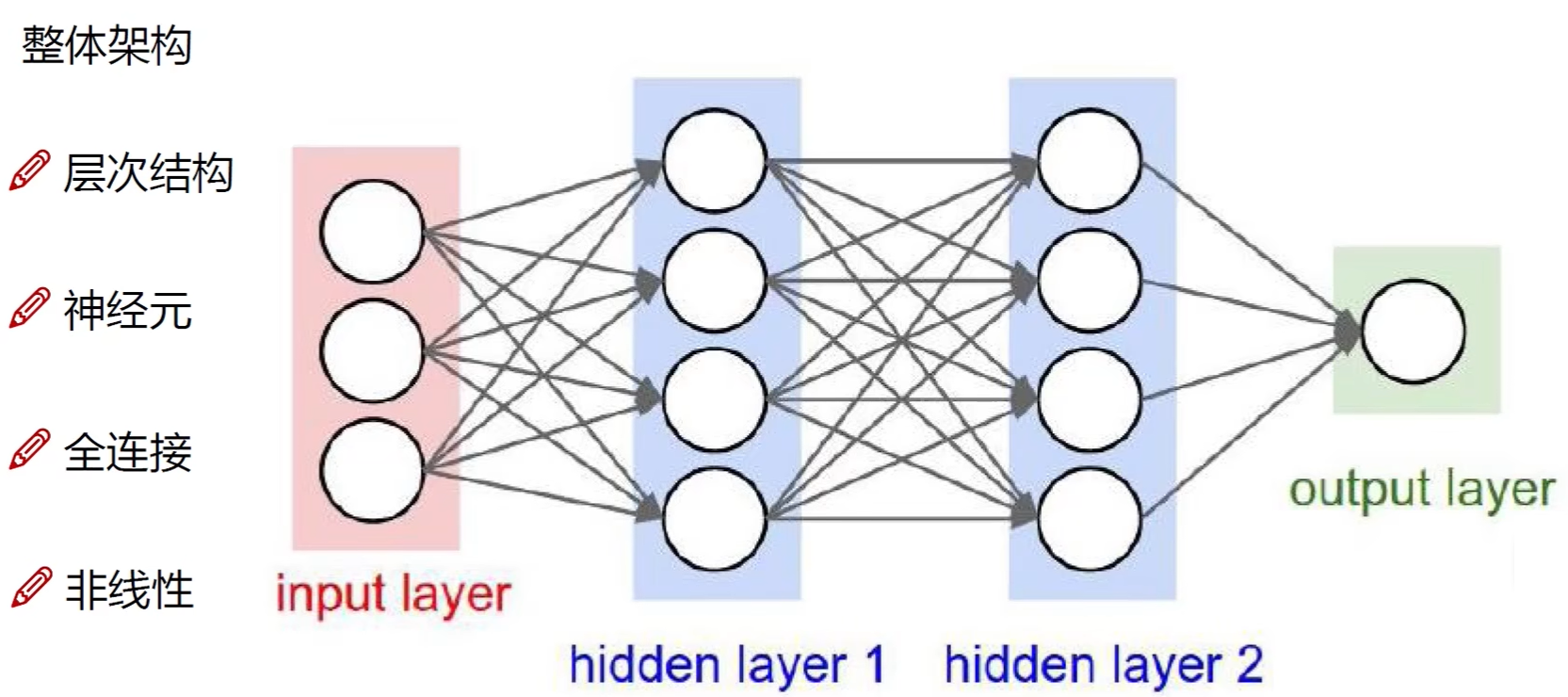
特点
- 堆叠:$f=W_3max(0,W_2max(0,W_1x))$,参数极多
- 神经元个数影响:神经元多,分类效果好
- 参数个数影响:参数多,拟合高
- 极大神经网络在适当正则化下不损害性能,拥有低偏差:惩罚力度小,拟合高;惩罚力度大,平稳
- 停滞区(plateaus)使学习过程慢
参数随机初始化
w[1] = np.random.randn((2, 2)) * 0.01
# [1]表示第一层 初始化 w 不能只设为 0, 否则会使得多个神经元工作对称一致 0.01使得学习速度更快
b[1] = np.zeros((2, 1))
# b 不会由于初始值为 0 产生对称问题/对称失效问题隐藏层工作
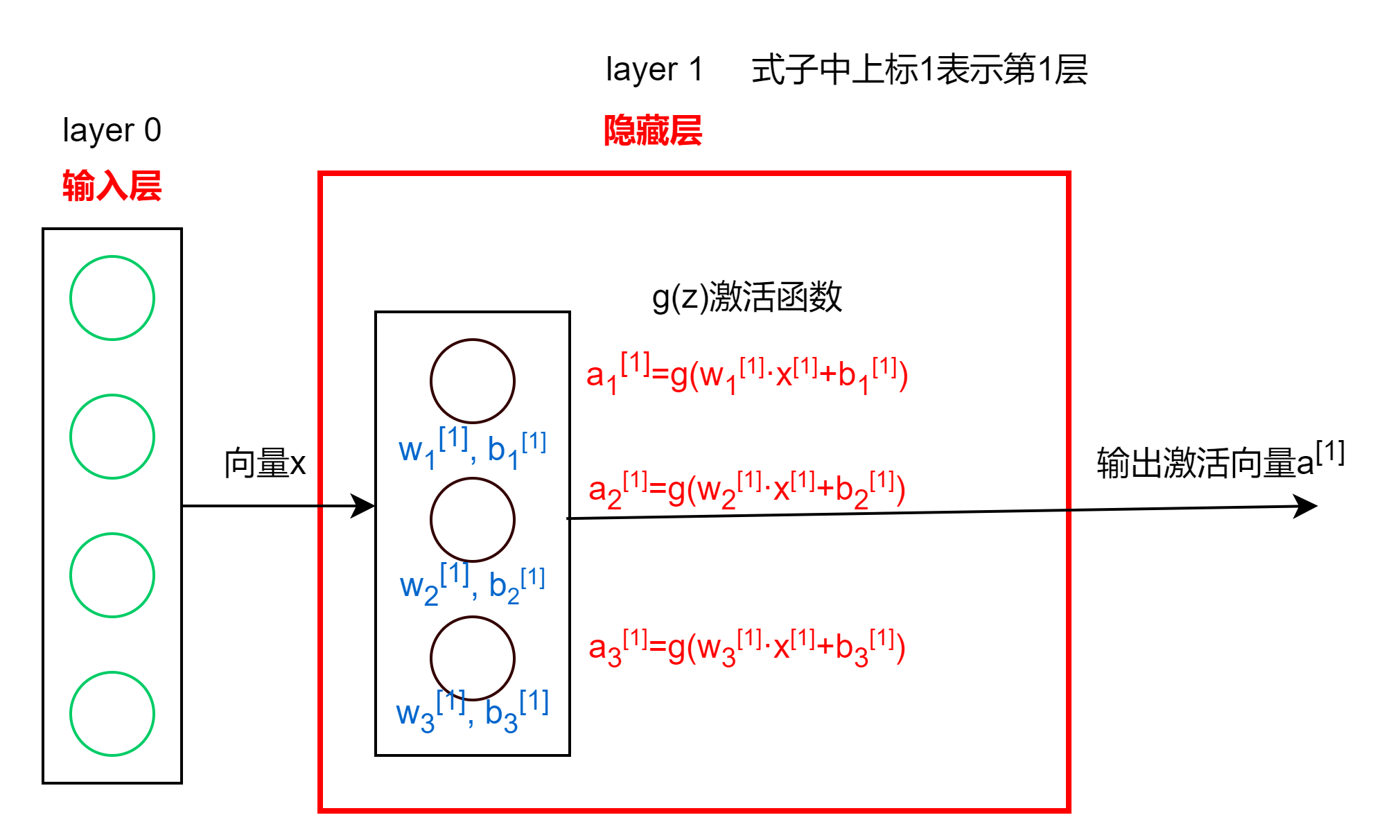
层类型
密集层(Dense Layer)
- 上一层的输出经过激活函数,得到该层每个神经元输出
卷积层(Convolutional Layer)
- 该层每个神经元只关注上一层输入的一部分,例如图像中抽取任意个像素块,可以相互重叠
- 计算快,更少训练集,不易过拟合
线性函数
- 输入到输出的映射:图片(32x32x3)经$f(x, W)=Wx+b$得到每个分类的得分,$x$为图片,$W$为权重参数,$b$为偏置参数
- 其中,共分N个类别,则W=Nx32x32x3=Nx3072,x=32x32x3x1=3072x1,两者矩阵相乘得到 Nx1 的不同类别的得分,b为Nx1
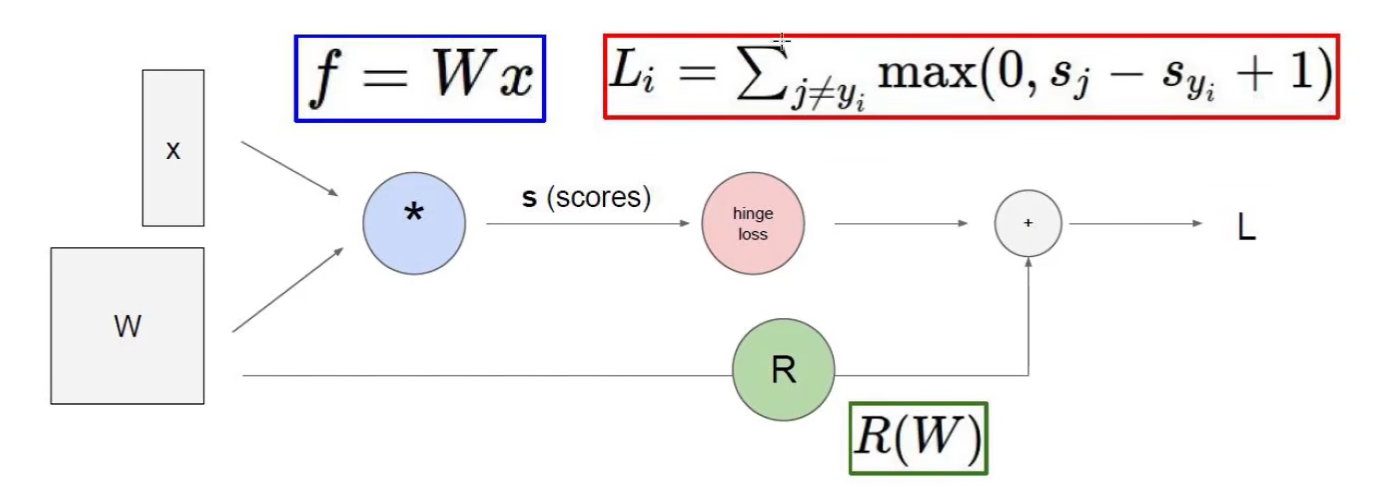
损失函数
- 举例:$L_i=\sum_{j\ne y_i}max(0,s_j-s_{y_i}+1)$,$s_j$是错误的,$s_{y_i}$是正确的
- 再加入正则化惩罚项防止过拟合:$L=\frac{1}{N}\sum_{i=1}^N\sum_{j\ne y_i}max(0,f(x_i;W)_j-f(x_i;W)_{y_i}+1)+\lambda R(W)$
- 其中$R(W)=\sum_k\sum_lW^2_{k,l}$
深度神经网络
- $n^{[l]}$表示第 l 层的神经元数 ,$a^{[l]}$表示第 l 层的激活函数
- $w^{[l]}$表示第 l 层中间值的权重,$b^{[l]}$表示第 l 层中间值的偏置值
- $z=g(a), \quad a=w\cdot x+b$
- $Z^{[l]}, A^{[l]},dZ^{[l]}, dA^{[l]}$矩阵: $(n^{[l]}, m)$,m为训练集数量
激活函数
模型输出的原始值转换为概率分布
- 线性激活函数:$g(z)=z$
- 全为线性激活函数使得神经网络等价于线性回归模型
- 隐藏层均为线性激活函数而输出层为sigmoid函数使得神经网络等价于逻辑回归模型
- 非线性:Sigmoid,Relu,tanh等
神经网络主要使用 Relu函数 (Rectified Linerar Unite:线性整流函数,非二元, 更快) 而不使用Sigmoid函数,Sigmoid函数会出现梯度消失现象( 两端平坦, 导致梯度下降慢, Relu只有一端平坦 )
Relu函数:$\sigma(x)=max(0,x)$
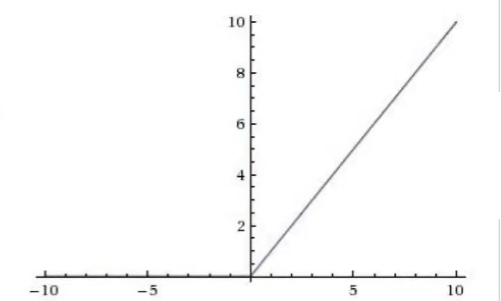
Leaky ReLU函数:$\sigma(x)=\begin{cases}x,,,x\gt 0\\alpha x,,,x\le 0\end{cases}$
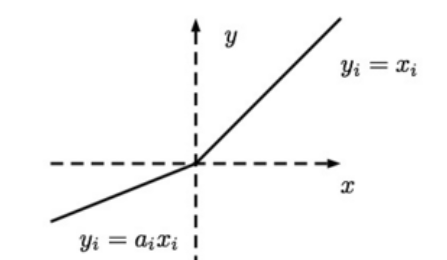
tanh函数:$\sigma(x)=tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$,具有居中数据效果
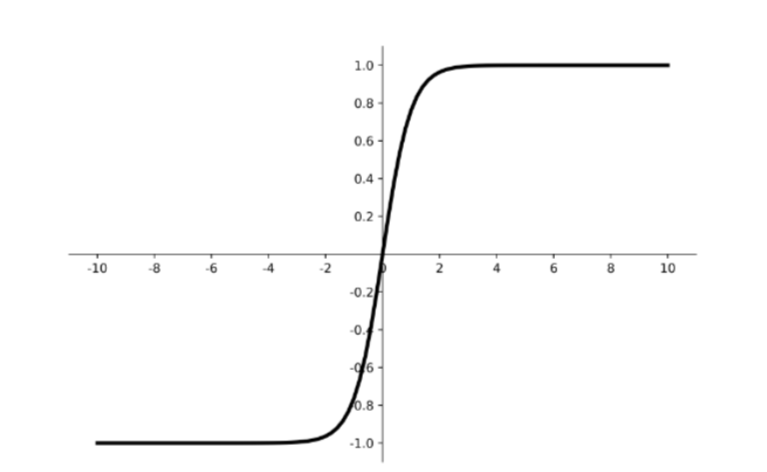
神经网络-激活函数选择
- 输出层:线性: y=+/- | Sigmoid: y=0/1 | Relu: y=0/+
- 隐藏层:默认选择Relu
正则化
Frobenius norm 正则化:$||\cdot||_F^2$
$\frac{\lambda}{2m}\sum_{l=1}^L||w^{[l]}||^2_F=\sum_{i=1}^{n^{[l-1]}}\sum_{j=1}^{n^{[l]}}(w_{ij}^{[l]})^2$
反向传播中:$dw^{[l]}=(from,,backprop) + \frac{\lambda}{m}w^{[l]}$
DROP-OUT 正则化
随机抽取一些神经元训练,解决过拟合,以某一概率选择
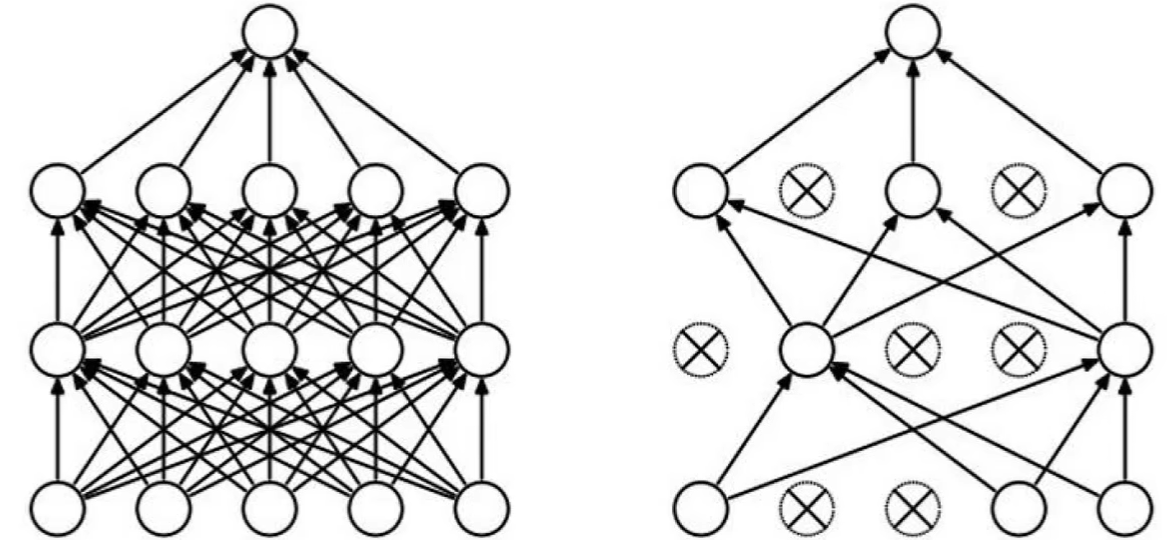
反向随机失活(Inverted dropout)
不依赖任何一个特征,所以权重将会更扩散
# dl: 布尔矩阵
dl = np.random.rand(al.shape[0], al.shape[1]) < keep-prob # keep-prob为留存概率值 0.8
al = np.myltiply(al, dl) # 可能有20%的将会为false
al /= keep-prob归一化
归一化输入
对训练集和测试集使用归一化,使用同样的均值及方差:
- 计算均值,每个值减去$\mu$,将均值$\mu$变为0
- 方差归一化,计算方差,每个样本除以$\sigma^2$,将方差变为1
梯度消失/爆炸
- 深层网络中
- 当权重 w 只比 1 或单位矩阵大一点,激活函数/梯度将会随 L 层指数级增长到爆炸
- 当权重 w 比 1 小一点,激活函数/梯度将会指数级减少到消失
权值初始化减轻梯度消失/爆炸
- Xavier初始化:Tanh 对随机生成的 w 参数$\cdot \sqrt\frac{1}{n^{[l]}}$,n 为特征/神经元数,l 为层数
- ReLu函数则:$\cdot \sqrt\frac{2}{n^{[l]}}$
批量归一化(Batch Norm)
隐藏层归一化,对隐藏单元的$z_{norm}^{(i)}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^2+\varepsilon}}$及$\tilde z^{(i)}=\gamma\cdot z_{norm}^{(i)}+\beta$归一化再输入激活函数,$\gamma, \beta$参数可由梯度下降调整
前向传播
输入到输出,从左往右,神经元数逐层减少,计算激活值及成本
使用指数函数扩大差异,再取平均值归一化:$P(Y=k|X=x_i)=\frac{e^{s_k}}{\sum_je^{s_j}}$,其中$s=f(x_i;W)$
计算损失值:$L_i=-logP(Y=y_i|X=x_i)$,P越接近1,log后越小
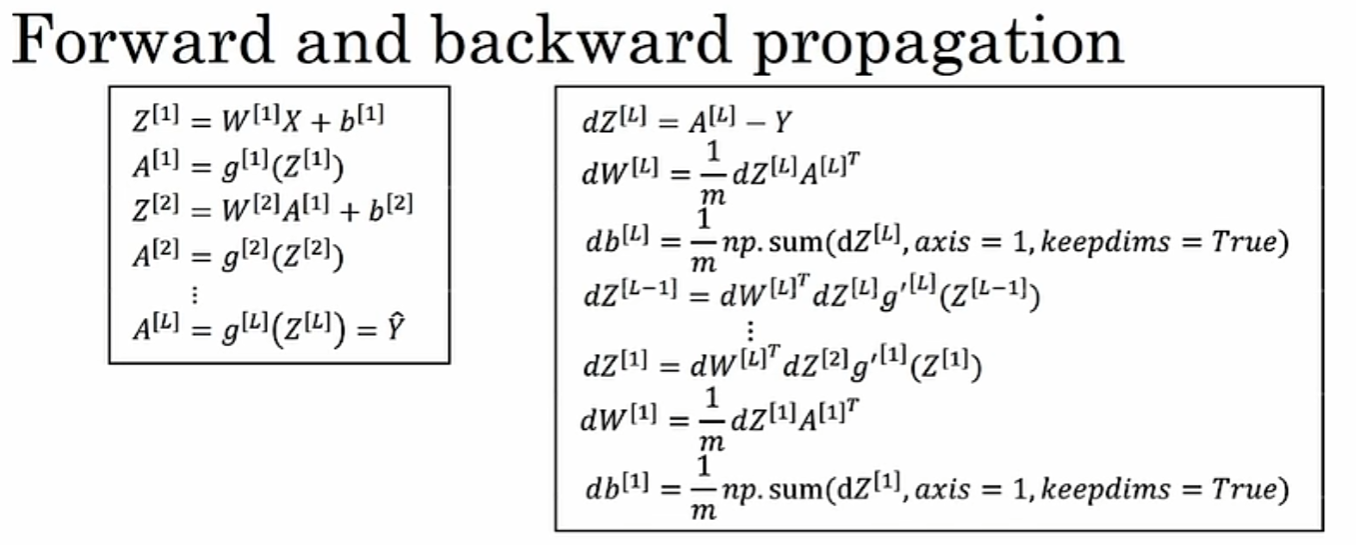
反向传播
梯度下降 链式法则:梯度一步步传播,参考偏导来计算 J 关于 w 和 b 参数的导数
反向的时候需要:正向时的每个中间结点的值都存储在中间结点
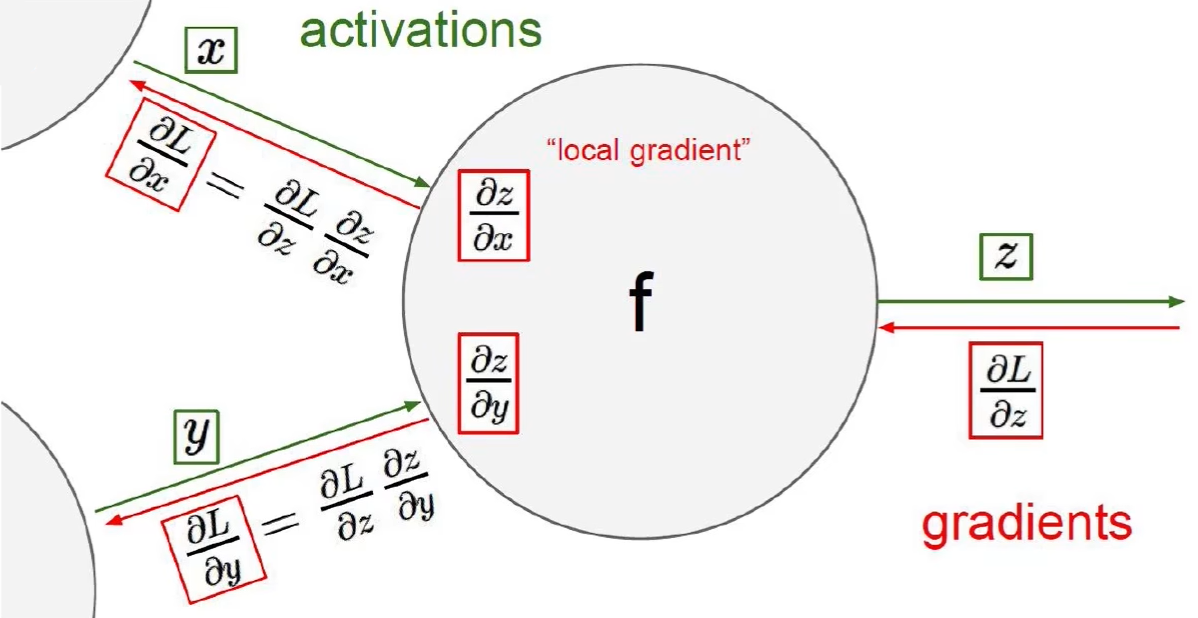
例子:
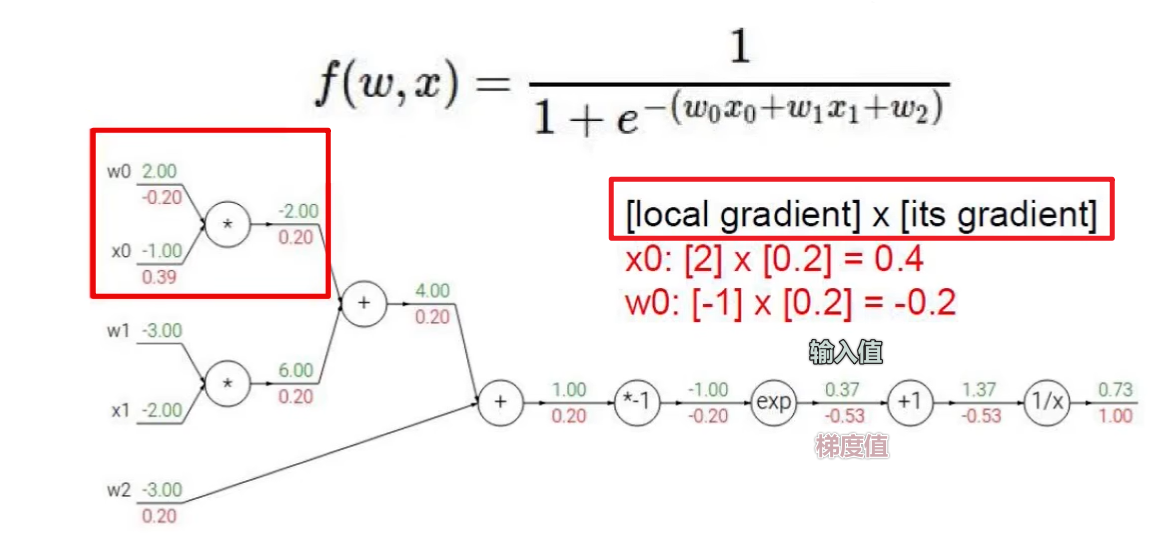
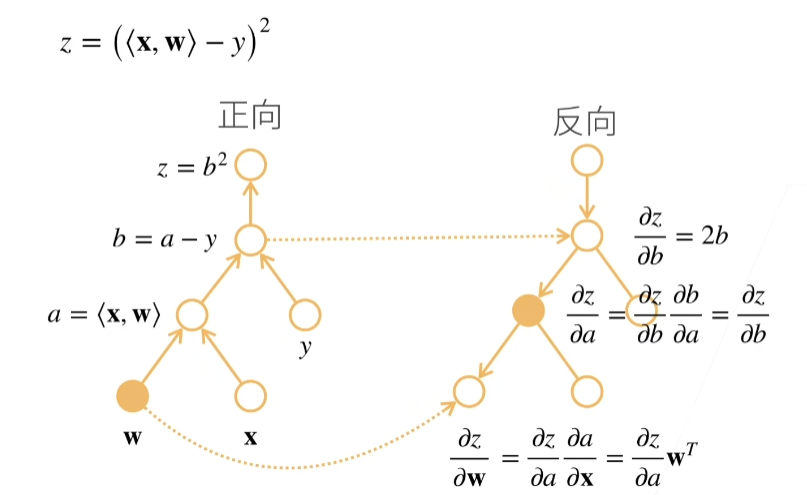
逻辑回归反向传播过程
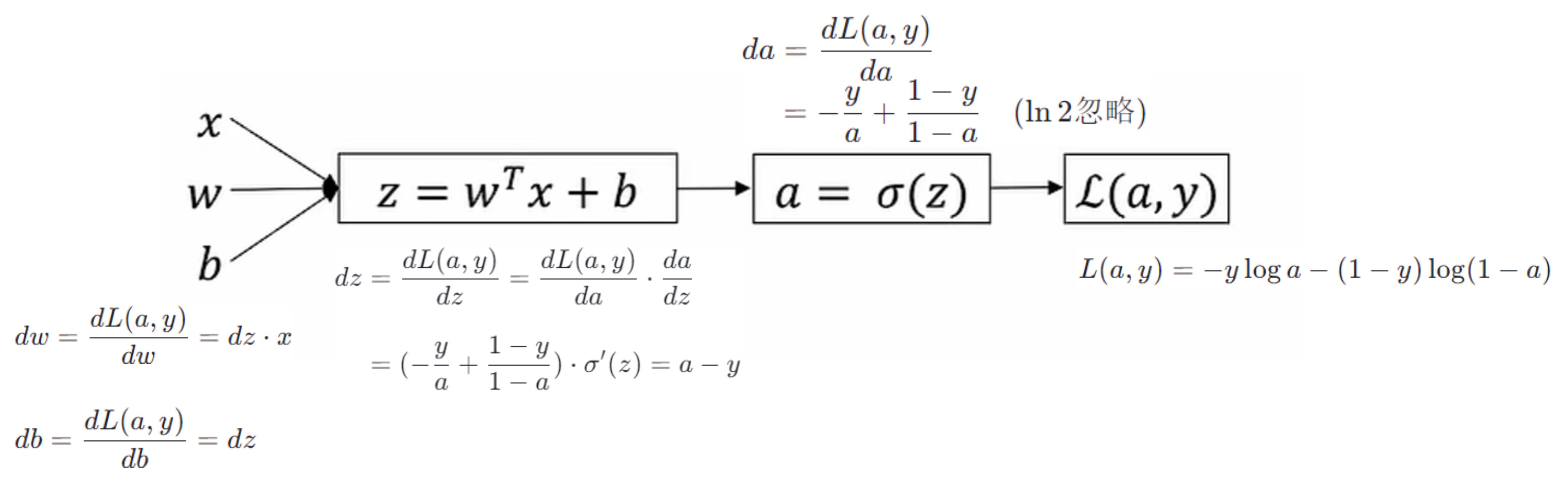
【调试】梯度检查:J 函数中的 $\theta$是向量中某个$\theta_i$
计算$d\theta_{approx}=\frac{J(\theta+\varepsilon)-J(\theta-\varepsilon)}{2\varepsilon}$,计算标准化后欧几里得距离$\frac{||d\theta_{approx}-d\theta||_2}{||d\theta_{approx}||_2+||d\theta||_2}$与$\varepsilon=10^{-7}$比较
指数加权滑动平均
有大体趋势的多噪声散点图使用:$V_t = \beta V_{t-1} + (1-\beta \theta_t)$做出平滑曲线,相当于取$\frac{1}{1-\beta}$天的平均值
偏差纠正
解决初期指数加权平均的值与真实值相差过大,使用$\frac{V_t}{1-\beta^t}$
