GPT-2复现学习
GPT-2复现学习
- from Andrej Karpathy
- 包含神经网络、反向传播、语言模型、多层感知机、分词器、复现 GPT-2
neural networks and backpropagation
micrograd
- 优先使用 micrograd 理解,理解导数
- 导数:
(f(x+h) - f(x)) / h
# 定义对象的官方字符串表示 Test(test=xxx, is_true='true')
def __repr__(self):节点数据结构
data存储实际数值_prev来存储子节点,(3+4=7,7中存储3和4)_op存储操作符lable代表变量名grad代表梯度
操作过程

a * b + c = L- 运算表达式构建正向传播的逻辑图
- 从后往前,通过导数定义计算梯度,取极小值 h,基于 h 更改当前节点值,计算出导数更新 grad
- 最终结果 L 的导数,对自身求导 grad = 1
- 往前传播
dL/dc,(f(d+h) - f(d)) / hdL/de,(f(e+h) - f(e)) / hdL/db,需要局部导数,链式法则de/dbdL/de,两者相乘
反向传播
- 最终值的梯度需要先设置为1
- 按照反向拓扑顺序对所有节点调用 backward 反向传播函数
- 加法:加法节点是梯度的分配器,由于该操作对每个节点的局部导数均为1,可通过导数定义得出,简单平分给加法两个子节点
- e 梯度为 1 乘以 L 梯度
- c 梯度为 1 乘以 L 梯度
- 乘法:
- b 梯度为 a 值乘以 e 梯度
- a 梯度为 b 值乘以 e 梯度
- tanh:根据求导公式得出两节点之间需要乘以的值
- 加法:加法节点是梯度的分配器,由于该操作对每个节点的局部导数均为1,可通过导数定义得出,简单平分给加法两个子节点
- 使用
+=来累计叠加梯度,解决节点重复交叉情况时覆盖梯度情况
pytorch
x = torch.Tensor([2.0]).double() # 单数据
x.requires_grad = True # 默认为 false
x.data.item() # 从包含一个元素的张量中提取值转换为 python 标量
x.grad.item() # 计算梯度神经网络
神经元
class Neuron(Module):
# nin 为输入个数
def __init__(self, nin, nonlin=True):
# 权重和偏置值随机初始化
self.w = [Value(random.uniform(-1,1)) for _ in range(nin)]
self.b = Value(0)
self.nonlin = nonlin
# __call__ 使得 x = [2.0, 3.0]; n = Neuron(2); n(x) 调用 __call__
def __call__(self, x):
act = sum((wi*xi for wi,xi in zip(self.w, x)), self.b)
return act.relu() if self.nonlin else act
def parameters(self): # 用于返回参数列表
return self.w + [self.b]神经元层
- 包含若干神经元,但互不连接
class Layer(Module):
# nout 为层中神经元个数
def __init__(self, nin, nout, **kwargs):
self.neurons = [Neuron(nin, **kwargs) for _ in range(nout)]
def __call__(self, x):
out = [n(x) for n in self.neurons] # 对每个神经元进行计算
return out[0] if len(out) == 1 else out
def parameters(self):
return [p for n in self.neurons for p in n.parameters()]多层感知机MLP
class MLP(Module):
# nouts 为 list(nout) 定义所有层尺寸
def __init__(self, nin, nouts):
sz = [nin] + nouts
self.layers = [Layer(sz[i], sz[i+1], nonlin=i!=len(nouts)-1) for i in range(len(nouts))]
def __call__(self, x):
for layer in self.layers:
x = layer(x)
return x
def parameters(self): # 获取所有参数
return [p for layer in self.layers for p in layer.parameters()]模型流程
x = [2.0, 3.0, -1.0]
n = MLP(3, [4, 4, 1])
n(x) # 3-4-4-1 神经网络- 已有神经网络可计算出预测值,且会有原本的最终值,通过损失来衡量两者差距
- 针对参数 w 和 b 的梯度若为负,对损失的影响也为负
- 输入不可变,改变参数调整值向最小化损失的方向走
梯度下降:反复进行前向传播、参数置零(防止叠加)、反向传播(计算梯度)、更新参数,神经网络将改善预测,其中更新参数为:
# 手动更新神经网络参数权重
for p in n.parameters(): # 获取所有参数
p.data += -0.01 * p.grad # 0.01 为学习率, 负号表示沿着梯度反方向更新为何往梯度下降方向走:因为梯度指向的是损失函数增长最快的方向
∂L/∂w为梯度- 梯度为正:减去正数 → 参数减小
- 梯度为负:减去负数 → 参数增加
- 梯度为正
- 如果增加参数 w,损失函数 L 会增加
- 如果减小参数 w,损失函数 L 会减小
- 梯度为负
- 如果增加参数 w,损失函数 L 会减小(因为梯度为负)
- 如果减小参数 w,损失函数 L 会增加
损失函数 L
↑
| 情况1:梯度为正
| ↗ 我们要往左走(减小w)
| ↗
| ↗
+----------→ 参数 w
损失函数 L
↑
| 情况2:梯度为负
| ↘ 我们要往右走(增加w)
| ↘
| ↘
+----------→ 参数 wlanguage modeling
makemore
- 一个基于字符级别的语言模型,根据名字数据集生成新名字,用于预测字符序列的下一个词
Bigram-二元语言模型
读取文件
words = open('names.txt', 'r').read().splitlines()通过前一个字符,预测下一个字符,对于名字集中每个名字,两两组合字符
for w in word[:4]: # 前4个名字
chs = ['<S>'] + list(w) + ['<E>'] # list 会返回一个包含所有字符的列表
# 后续无需使用两个标记而只用一个 . (由于 <E>x 和 x<S> 频率均为 0)
for ch1, ch2 in zip(chs, chs[1:]:
bigram = (ch1, ch2)
b[bigram] = b.get(bigram, 0) + 1 # 字典计算频率排序:sorted(b.items(), key = lambda kv : kv[1])
获取字符-数字映射
chars = sorted(list(set(''.join(words))))
stoi = {s:i+1 for i,s in enumerate(chars)}
# stoi['<S>'] = 26
# stoi['<E>'] = 27
stoi['.'] = 0
itos = {i:s for s,i in stoi.items()}利用张量:获取的 N 矩阵每个值为两个字母前后组合的频率
import torch
# 初始为 0 的 27*27 矩阵
N = torch.zeros((27, 27), dtype=torch.int32)
# N[0, 0] = 1 赋值
# N[0].float() 取出第一行 求和为.sum()
for w in words:
chs = ['.'] + list(w) + ['.'] # 收缩 .. 到 N[0,0]
for ch1, ch2 in zip(chs, chs[1:]):
ix1 = stoi[ch1]
ix2 = stoi[ch2]
N[ix1, ix2] += 1 # 第一列为以字母结尾, 第一行为以字母开头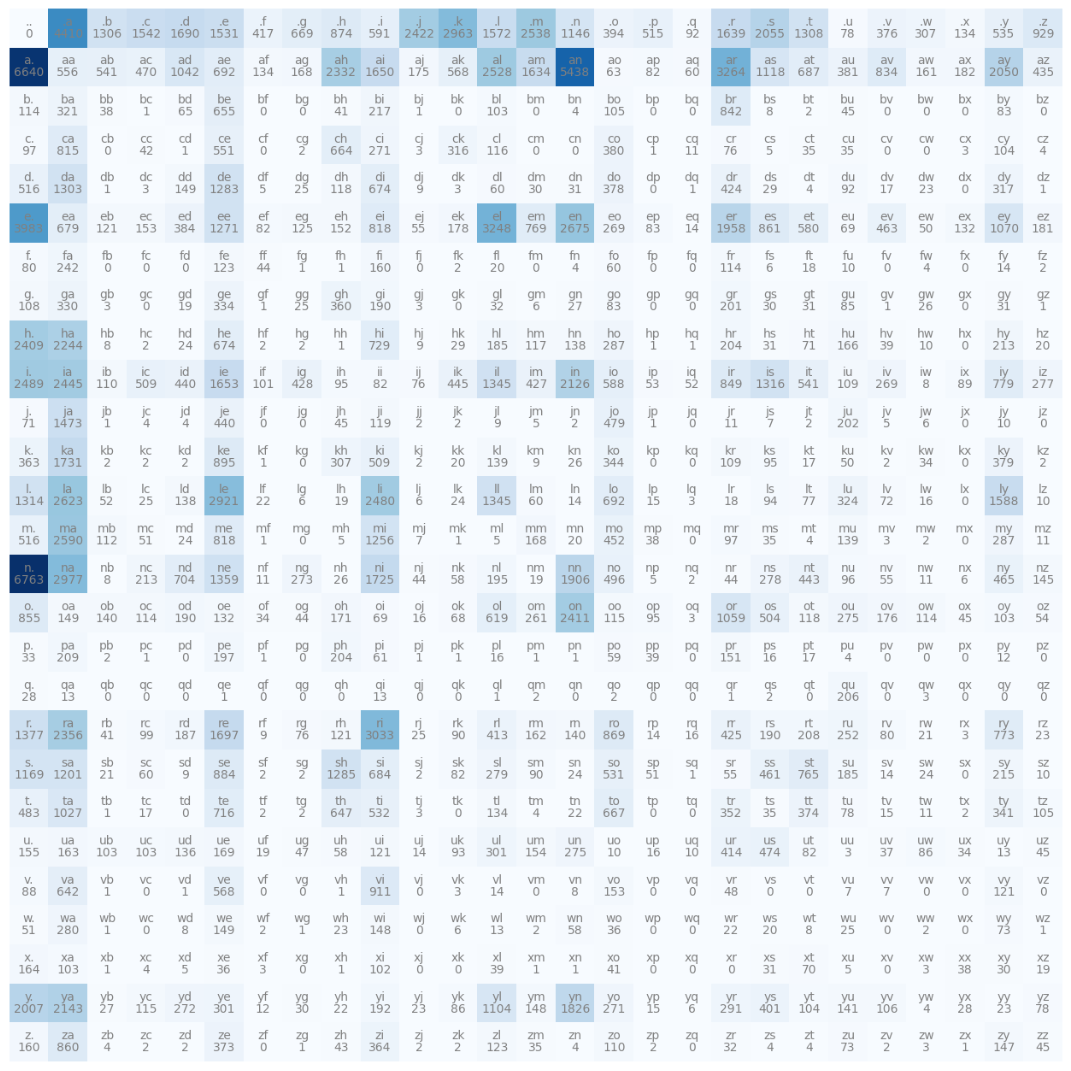
# 绘图方法
import matplotlib.pyplot as plt
%matplotlib inline
plt.figure(figsize=(16, 16))
plt.imshow(N, cmap='Blues')
for i in range(27):
for j in range(27):
chstr = itos[i] + itos[j]
plt.text(j, i, chstr, ha="center", va="bottom", color='gray')
plt.text(j, i, N[i, j].item(), ha="center", va="top", color='gray')
plt.axis('off');多项式概率分布中采样获取样本(torch.multinomial)
- 给定一个概率分布,根据这些概率分布返回整数
# 随机生成器
g = torch.Generator().manual_seed(xxx) # 确保随机数生成是可重现的
p = torch.rand(3, generator=g) # 生成包含3个随机数的张量
p / p.sum() # 归一化获取概率
# 采样 接受概率分布的张量, 根据该概率分布请求 20 个样本, 样本满足该概率分布
# replacement=True: 抽取一个元素后放回可抽取的索引列表中, 可再次抽取
ix = torch.multinomial(p, num_samples=20, replacement=True, generator=g)
# tensor([1,1,2,0,0,2,1,1,0,0,0,1,1,0,0,1,1,0,0,1]) 实际获取 p 大小的随机一个索引
itos[ix] # 获取字符训练二元模型 - 生成名字
g = torch.Generator().manual_seed(xxx)
out = []
ix = 0
while True:
# p = N[ix].float() # 遍历矩阵每一行 训练二元模型
# p = p / p.sum() # 归一化
# 优化上面两行
p = P[ix]
# p = torch.ones(27) / 27.0 均匀分布, 即完全未经训练的模型, 获取的名字效果很差
ix = torch.multinomial(p, num_samples=1, replacement=True, generator=g).item() # 选取下一个索引行
out.append(itos[ix])
if ix == 0:
break
print(''.join(out)) # 获取生成结果优化:使用矩阵实现并行,且利用广播机制
- keepdim:保持变化后输出张量的维度数不变( 34 → 1n 而不是 3*4 → n )
P = N.float() # P.shape: torch.Size([27, 27])
# 模型平滑: P = (N+1).float()
P /= P.sum(1, keepdim=True) # 27*1 广播成 27*27 计算
# 操作解释
P.sum(0, keepdim=True) # 沿着维度 0 (行方向列求和), (1, 27) 行向量
P.sum(1, keepdim=True) # 沿着维度 1 (列方向行求和), (27, 1) 列向量评估模型质量
- 对于真实的名字集中两两组合的字符概率,应该越高越好,且概率乘积也应越高(越接近1)
- 越接近1,对数越接近0
- 利用负对数似然,即
-logP,作为损失函数:越低可达到 0,效果越好,越高效果越差
log_likelihood = 0.0
n = 0 # 均值
for w in words[:3]:
chs = ['.'] + list(w) + ['.']
for ch1, ch2 in zip(chs, chs[1:]):
ix1 = stoi[ch1]
ix2 = stoi[ch2]
prob = P[ix1, ix2]
logprob = torch.log(prob) # log(a*b*c) = log(a) + log(b) + log(c)
log_likelihood += logprob
n += 1
print(f'{ch1}{ch2}: {prob:.4f} {logprob:.4f}')
print(f'{-log_likelihood /n}') # 平均负对数似然训练任务:找到使得负对数似然损失最小的参数
- 损失越小,模型越好,因为其给训练的数据分配了高的概率
考虑一个情况,若jq两个单词连接的概率为0,会导致对数为无穷大,解决该问题的方法为模型平滑,给矩阵 N 的每个值加入一个值 1,再计算概率矩阵 P
Bigram-神经网络框架
接下来,需要将双字母字符级语言模型转换成神经网络框架
- 输入一个单字符,带有权重/参数的神经网络,输出下一个字符的概率分布,猜测可能跟随的输入字符
xs, ys = [], []
for w in words[:1]: # emma
chs = ['.'] + list(w) + ['.']
for ch1, ch2 in zip(chs, chs[1:]):
ix1 = stoi[ch1]
ix2 = stoi[ch2]
xs.append(ix1)
ys.append(ix2)
xs = torch.tensor(xs) # tensor([ 0, 5, 13, 13, 1]) .emma
ys = torch.tensor(ys) # tensor([ 5, 13, 13, 1, 0]) emma.one-hot encoding:热编码,将整数编码成向量
- 第整数位设置为 1,其余为 0,一个字母为 1x27 向量
import torch.nn.functional as F
xenc = F.one_hot(xs, num_classes=27).float() # shape: (5, 27)随机初始化权重参数
W = torch.randn((27, 27)) # 从正态分布中取数 第二个 27 为 27 个神经元
# 设置梯度为 0 方法: W.grad = None
# [
# [w₀₀, w₀₁, w₀₂, ..., w₀₂₆], # 输入字符'.'的权重向量
# [w₁₀, w₁₁, w₁₂, ..., w₁₂₆], # 输入字符'a'的权重向量
# ...
# [w₂₆₀, w₂₆₁, ..., w₂₆₂₆] # 输入字符'z'的权重向量
# ]- 每行对应一个输入字符的权重参数
- 每列对应一个输出神经元
W[i,j]表示当输入字符为i时,对输出字符j的"贡献权重"
xenc @ W # 矩阵乘法: (5, 27) * (27, 27) = (5, 27)结果矩阵每个值意思:对于创建的每一个神经元,这些神经元在每一个输入例子上的激活率是多少,即每个字符经过神经网络后的"原始分数”,通过第 m 个输入和 W 矩阵的第 n 列实现
[
[w₀₀, w₀₁, w₀₂, ..., w₀₂₆], # 输入'.'时的神经元激活值
[w₅₀, w₅₁, w₅₂, ..., w₅₂₆], # 输入'e'时的神经元激活值
[w₁₃₀, w₁₃₁, ..., w₁₃₂₆], # 输入'm'时的神经元激活值
[w₁₃₀, w₁₃₁, ..., w₁₃₂₆], # 输入'm'时的神经元激活值
[w₁₀, w₁₁, w₁₂, ..., w₁₂₆] # 输入'a'时的神经元激活值
]输入:27 维
经过 27 个神经元,只经过 wx 即,线性层
转换
- 指数后,负数变成 0 - 1 间的数,正数变成 > 1 的数
- softmax:指数运算后,除法且归一化处理,像概率分布一样,输出总和为 1
$$ \frac{e^{z_i}}{\sum^K_{j=1}(e^{z_j})} $$
logits = xenc @ W # 假设为 log(counts) 对数计数
# 以下两行被称为 softmax
counts = (xenc @ W).exp() # 等效于 N 矩阵, exp(log(counts)) 即计数 counts
# 每一行大致是下一个字符的计数
probs = counts / counts.sum(1, keepdims=True) # 概率矩阵随着调整优化权重 W,对于任何输入的字符会得到不同的概率输出
- 以下为分别表示输入某个字符 x 后,预测另一个字符 y 时的概率,即神经网络分配给正确下一个字符的概率
probs[0, 5]:当输入是.时,预测e的概率probs[1, 13]:当输入是e时,预测m的概率probs[2, 13]:当输入是m时,预测m的概率probs[3, 1]:当输入是m时,预测a的概率probs[4, 0]:当输入是a时,预测.的概率- 两种方式获取值相同,形式不同
probs[0, 5], probs[1, 13], probs[2, 13], probs[3, 1], probs[4, 0]
# (tensor(), tensor(), ...)
probs[torch.arange(5), ys]
# tensor([xx, xx, ...]) 批量概率提取计算损失
# 负平均对数似然损失
loss = -probs[torch.arange(5), ys].log().mean()
loss.backward() # 反向传播神经网络 - 完整流程
- 加入正则化损失,类似于模型平滑
(W**2).mean(),对每个元素平方,负数正数均转换为正值,惩罚权重大的值,鼓励权重值接近0,使得分布更加稳定平滑,而不会受到类似噪声的极端值数据的影响;防止过拟合:完美拟合训练数据
xs, ys = [], []
for w in words:
chs = ['.'] + list(w) + ['.']
for ch1, ch2 in zip(chs, chs[1:]):
ix1 = stoi[ch1]
ix2 = stoi[ch2]
xs.append(ix1)
ys.append(ix2)
xs = torch.tensor(xs)
ys = torch.tensor(ys)
num = xs.nelement()
print("number of examples: ", num)
g = torch.Generator().manual_seed(xx)
W = torch.randn((27, 27), generator=g, requires_grad=true)
# 梯度下降
for k in range(10):
# 前向传播
xenc = F.one_hot(xs, num_classes=27).float()
logits = xenc @ W
counts = (xenc @ W).exp()
probs = counts / counts.sum(1, keepdims=True)
# 加入L2正则化 0.01为正则化强度
loss = -probs[torch.arange(5), ys].log().mean() + 0.01*(W**2).mean()
# 反向传播
W.grad = None
loss.backward() # W.grad 查看情况, (27, 27)
print(loss.item()) # 期望达到对原本名字集 words 计算得到的负平均对数似然损失相近的值
# 更新
W.data += -0.1 * W.grad # 0.1 学习率最终测试训练的神经网络效果
g = torch.Generator().manual_seed(xx)
for i in range(5):
out = []
ix = 0
while True:
# BEFORE:
# p = P[ix]
# NOW: 取 ix 编码为 one-hot 编码
xenc = F.one_hot(torch.tensor([ix]), num_classes=27).float() # (1, 27)
logits = xenc @ W # (1, 27) * (27, 27) -> (1, 27)
counts = logits.exp()
p = counts / counts.sum(1, keepdims=True) # p: (1, 27)
# 每个值表示当前值为 x , 下一个值为 27 个字符中每个的概率
# 取出某个字符的索引值, 0 ~ 26, 输出形状 (1, 1)
# 使用随机采样可以增加多样性, 如: q 可以结合 a,u, 但贪心则使得 q 可能一直和一个字母结合
ix = torch.multinomial(p, num_samples=1, replacement=True, generator=g).item()
out.append(itos[ix])
if ix == 0:
break
print(''.join(out))MLP Multilayer Perceptron
模型结构梳理
Bigram 只考虑了一个字符的上下文,若增加上下文,上下文组合矩阵将会成指数级增长
- 参考 MLP(https://www.jmlr.org/papers/volume3/bengio03a/bengio03a.pdf)实现的词级语言模型,实现字符级的语言模型,有 17000 个可能的词
- 每个词关联一个 30 维特征向量,嵌入到一个 30 维空间,首先随机初始化,接着通过传播来调整单词的嵌入,训练神经网络过程中,这些点、向量会在空间中移动
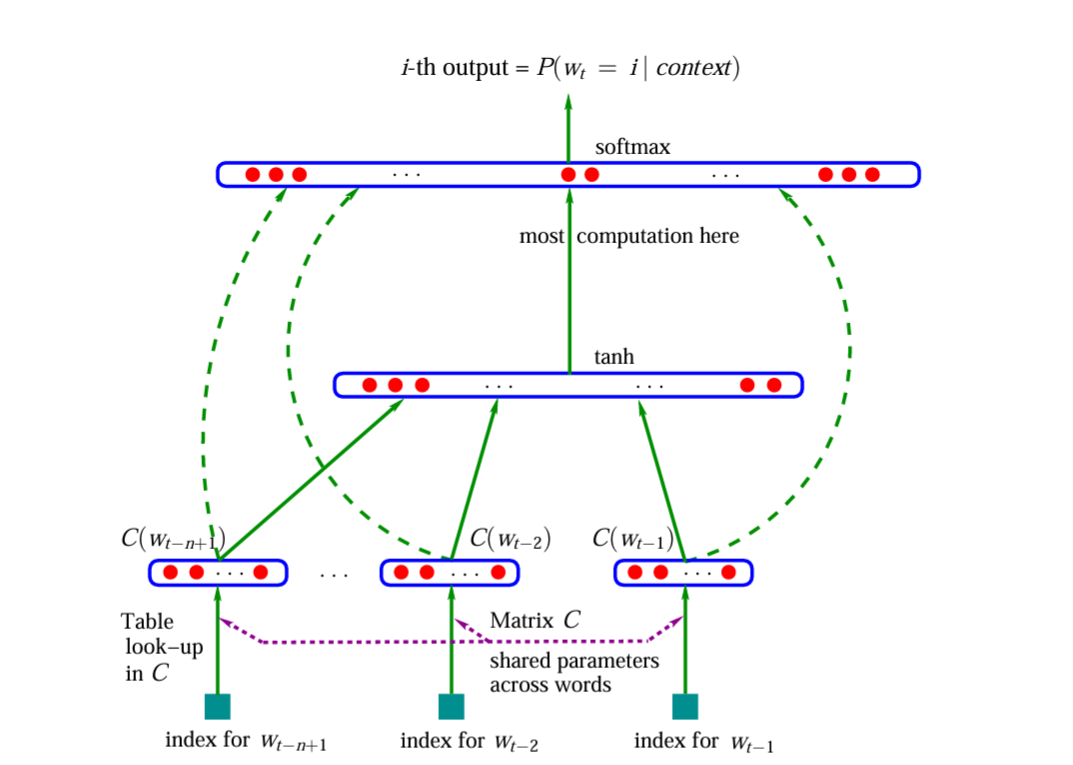
取前 3 个单词,预测第 4 个单词
- 输入单词的索引,根据查找表 C 找出对应的 30 维嵌入向量,3 个单词 90 个神经元输入
- 隐藏层大小为超参数
- 最后一层为 17000 个输出,softmax 层,每一个 logits 被指数化,所有结果会被归一化,总和为1 1,获取序列中下一个单词的良好概率分布
初始化
words = open('names.txt', 'r').read().splitlines()
chars = sorted(list(set(''.join(words))))
stoi = {s:i+1 for i, s in enumerate(chars)}
stoi['.'] = 0
itos = {i:s for s, i in stoi.items()}数据集构建
block_size = 3 # 上下文长度, 使用多少来预测下一个
X, Y = [], []
for w in words[:5]: # 完整数据集: 228000
context = [0] * block_size
for ch in w + '.':
ix = stoi[ch]
X.append(context)
Y.append(ix)
print(''.join(itos[i] for i in context), '--->', itos[ix])
context = context[1:] + [ix]
X = torch.tensor(X) # 示例 shape (32, 3), 32 表示目前的数据集大小
Y = torch.tensor(Y) # 标签 shape (32)
# ... ---> e
# ..e ---> m
# .em ---> m
# emm ---> a
# mma ---> .随机初始化嵌入矩阵 C
C = torch.randn((27, 2)) # 27 个字符每一个均有一个 2 维嵌入
# 取出某一行的方法: 以下两种均可
C[5]
F.one_hot(torch.tensor(5), num_classes=27).float() @ C # 类似屏蔽第5行以外的所有值
# 获取 X 的嵌入向量
emb = C[X] # shape: [32, 3, 2] 输入为 3*2 = 6 个神经元权重矩阵
W1 = torch.randn((6, 100)) # 中间假设 100 个神经元
b1 = torch.randn(100)需要使得嵌入向量和权重矩阵相乘:[32, 3, 2] 和 [6, 100] 如何结合
emb[:, 0, :], emb[:, 1, :], emb[:, 2, :] # 分别获取第 1, 2, 3 个单词的 (32, 2) 嵌入向量
# 在维度 1(第二个维度) 上连接, 最终为 (32, 6) shape
torch.cat([emb[:, 0, :], emb[:, 1, :], emb[:, 2, :]], 1)
# 优化
torch.cat(torch.unbind(emb, 1), 1) # (32, 6)
# 优化 使用 view 将底层的一维数组看做不同的视图
emb.view(32, 6)
# 隐藏层计算, 得到 shape: (32, 100)
h = torch.tanh(emb.view(-1, 6) @ W1 + b1) # -1 自动推断最终输出层
W2 = torch.randn((100, 27)) # 输出 27 个概率
b2 = torch.randn(27)
logits = h @ W2 + b2 # (32, 27)
counts = logits.exp()
prob = counts / counts.sum(1, keepdims=True) # shape: (32, 27)
prob[torch.arrange(32), Y)
# 获取给出权重设置下,由神经网络分配给序列中正确字符的当前概率, 每行 Y 标签对应的概率, 理想情况概率均为 1
# 损失获取
loss = -prob[torch.arrange(32), Y).log().mean()
# 优化损失 loss, 交叉熵得到结果一致, 优于上一行损失获取, 底层更加稳定
loss = F.cross_entropy(logits, Y)完整流程
# 数据集
X.shape, Y.shape
g = torch.Generator().manual_seed(xxx)
C = torch.randn((27, 2), generator=g) # 嵌入向量为 2 维
W1 = torch.randn((6, 100), generator=g)
b1 = torch.randn(100, generator=g)
W2 = torch.randn((100, 27), generator=g)
b2 = torch.randn(27, generator=g)
parameters = [C, W1, b1, W2, b2]
sum(p.nelement() for p in parameters) # 参数总数量
for p in parameters:
p.requires_grad = True
for _ in range(10):
# 前向传播
emb = C[X]
h = torch.tanh(emb.view(-1, 6) @ W1 + b1)
logits = h @ W2 + b2
loss = F.cross_entropy(logits, Y)
print(loss.item()) # 最终稳定在 0.25 左右 实际可能导致过拟合
# 反向传播
for p in parameters:
p.grad = None
loss.backward()
# 更新
for p in parameters:
p.data += -0.1 * p.grad无法达到零损失,由于数据集中开头的[0, 0, 0]: . . . 可以预测任何一个字符,所以无法完全过拟合使得损失值精确到零
... ---> e # 无法导致完全预测
emm ---> a # 这类数据可以较好拟合
# 对比下两行预测可看出以上结论
# (32, 27) 沿着每一行,找出该行的最大值: 即每个输入数据预测最大概率对应的概率值和对应的字符索引
logits.max(1)
Y小批量处理
- 一般情况下不会一直选取整个数据集进行迭代的前向传播和反向传播
- 所以随机选取数据集的一部分,一小批量进行前向传播、反向传播、更新
# 生成 32 个介于 0 和 5 之间的数字
torch.randint(0, 5, (32, ))
# 生成 32 个索引到数据集的整数, 最小批次此时为 32
torch.randint(0, X.shape[0], (32, ))优化处理,与之前相比运行速度加快,快很多
for _ in range(100):
# 小批量
ix = torch.randint(0, X.shape[0], (32, ))
# 前向传播
emb = C[X[ix]] # 只获取 32 行 (32, 3, 2)
h = torch.tanh(emb.view(-1, 6) @ W1 + b1)
logits = h @ W2 + b2
loss = F.cross_entropy(logits, Y[ix])
# 反向传播
for p in parameters:
p.grad = None
loss.backward()
# 更新
for p in parameters:
p.data += -0.1 * p.grad
print(loss.item()) # 最终损失值在 2.5 左右徘徊, 该损失值只是小批次的损失值
# 所有数据集损失
emb = C[X]
h = torch.tanh(emb.view(-1, 6) @ W1 + b1)
logits = h @ W2 + b2
loss = F.cross_entropy(logits, Y)学习率调整
一般学习率在 -0.001 ~ -1 之间
torch.linspace(0.001, 1, 1000) # 生成 1000 个介于 0.001 和 1 之间的数字, 等差数列
lre = torch.linspace(-3, 0, 1000) # 使用指数队列
lrs = 10**lre # 10 的 lre 次方, 用于大致搜索确定的候选学习率, 按指数步进- 使用学习率索引
lri = []
lossi = []
for i in range(1000):
# 小批量
ix = torch.randint(0, X.shape[0], (32, ))
# 前向传播
emb = C[X[ix]] # 只获取 32 行 (32, 3, 2)
h = torch.tanh(emb.view(-1, 6) @ W1 + b1)
logits = h @ W2 + b2
loss = F.cross_entropy(logits, Y[ix])
# 反向传播
for p in parameters:
p.grad = None
loss.backward()
# 更新
lr = lrs[i] # 学习率
for p in parameters:
p.data += -lr * p.grad
# 记录
# lri.append(lr) 第一种
lri.append(lre[i]) # 第二种, 指数队列
lossi.append(loss)图片绘制
① 直接学习率
plt.plot(lri, lossi)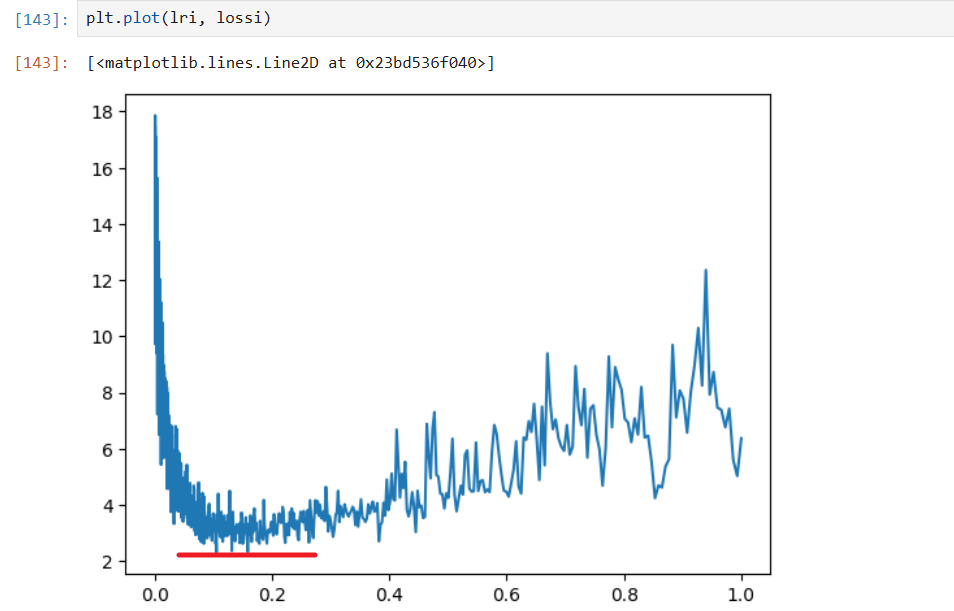
② 指数,选取合适的学习率指数,即 -1 左右,10^-1=0.1
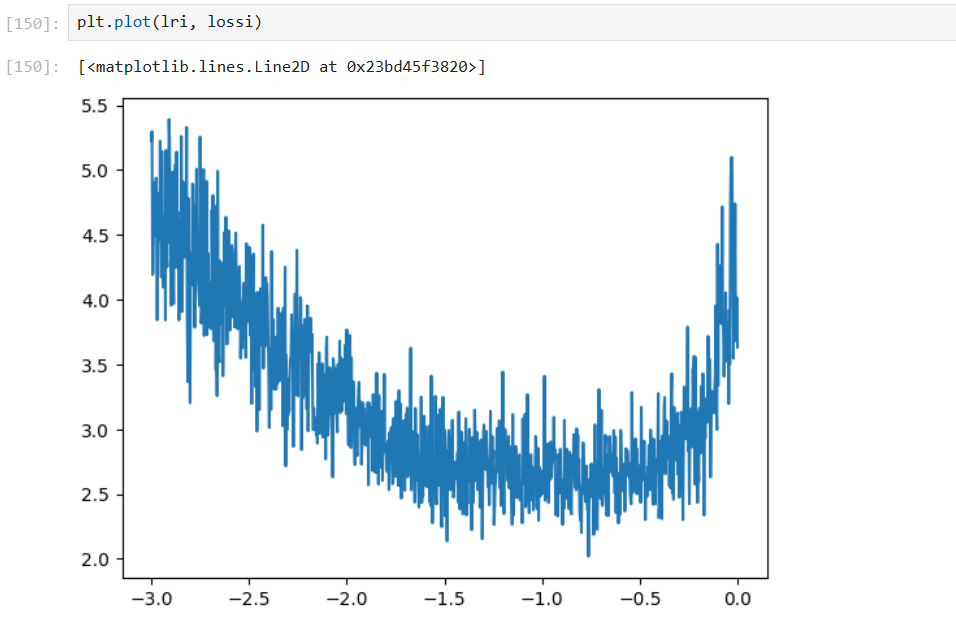
**学习率衰减:**训练后期阶段,降低十倍学习率,有几率将损失降到 2.34
数据集切分
随着神经网络容量增长,开始有能力过拟合数据集,泛化能力很低,所以一般会将数据集切分为
- 训练集 80% 用于训练权重参数
- 开发/验证集 10% 用于训练超参数
- 测试集 10% 最终评估性能
# 构建数据集
def build_dataset(words):
block_size = 3
X, Y = [], []
for w in words:
context = [0] * block_size
for ch in w + '.':
ix = stoi[ch]
X.append(context)
Y.append(ix)
context = context[1:] + [ix]
X = torch.tensor(X)
Y = torch.tensor(Y)
return X, Y
# 拆分数据集
import random
random.seed(xx)
random.shuffle(words)
n1 = int(0.8*len(words))
n2 = int(0.9*len(words))
Xtr, Ytr = build_dataset(words[:n1])
Xdev, Ydev = build_dataset(words[n1:n2])
Xte, Yte = build_dataset(words[n2:])- 训练集训练完后,使用开发集和全集来评估损失值,若基本相等说明未过拟合
- 由于网络模型规模小,使得处于的是欠拟合状态
扩大规模
- 尝试增加隐藏层的神经元数量,从 100 增加到 300
- 且加入跟踪 step 情况
lri = []
lossi = []
stepi = []
for i in range(30000):
# 小批量
ix = torch.randint(0, Xtr.shape[0], (32, ))
# 前向传播
emb = C[Xtr[ix]] # 只获取 32 行 (32, 3, 2)
h = torch.tanh(emb.view(-1, 6) @ W1 + b1)
logits = h @ W2 + b2
loss = F.cross_entropy(logits, Ytr[ix])
# 反向传播
for p in parameters:
p.grad = None
loss.backward()
# 更新
lr = 0.1 # 学习率
for p in parameters:
p.data += -lr * p.grad
# 记录
stepi.append(i)
lossi.append(loss.item())
plt.plot(stepi, lossi)学习率为 0.05
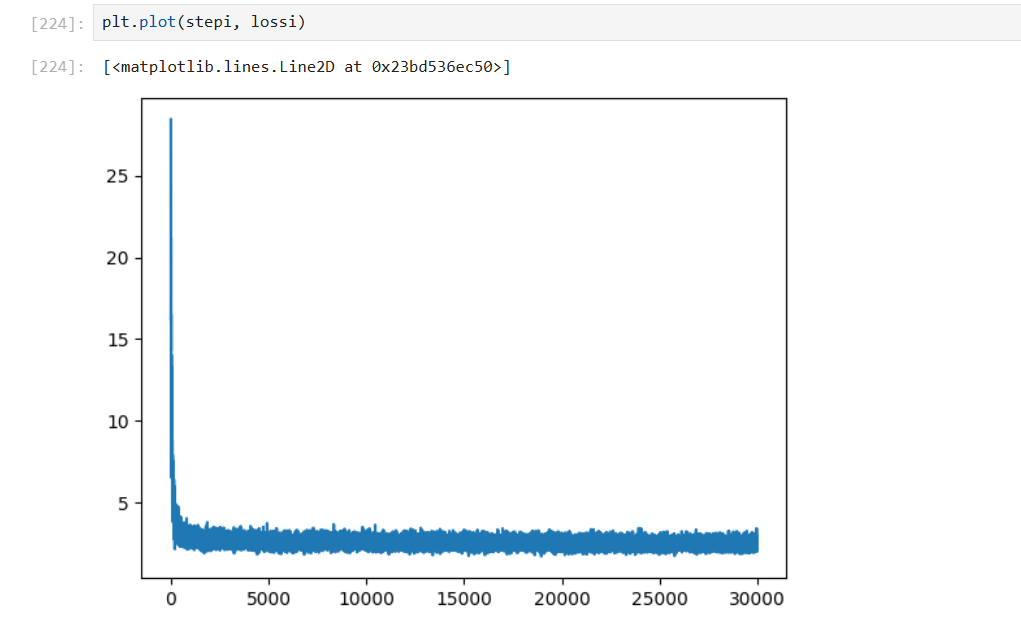
学习率为 0.1
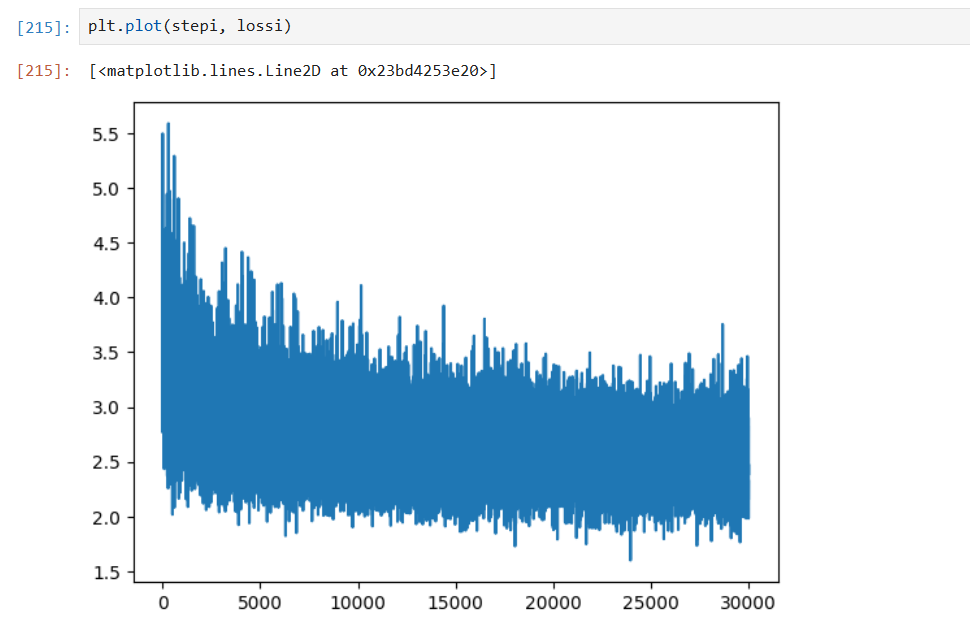
震荡很多:可能批量大小太小,导致训练噪声过多。
可尝试减少学习率,继续迭代,依旧在震荡,可能原因:嵌入向量维度太小,2 维限制了性能
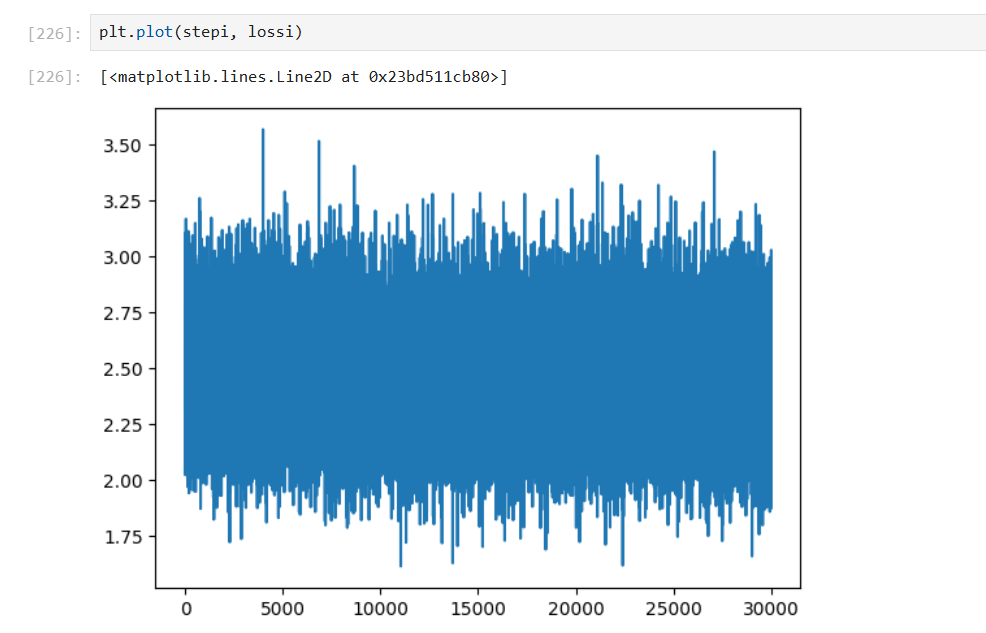
训练集和验证集损失比较
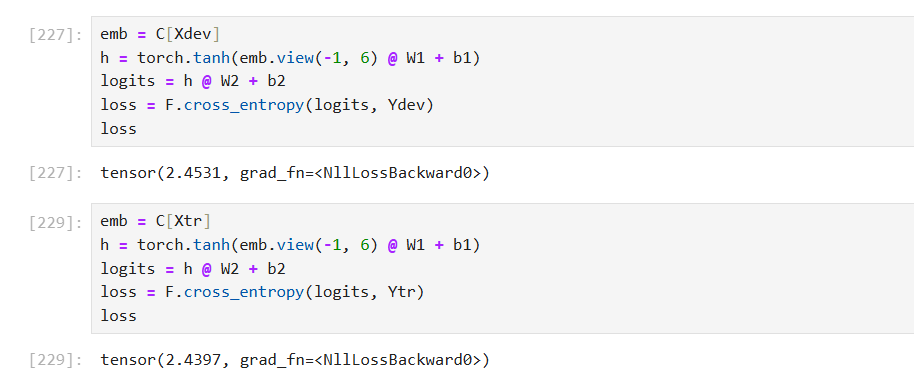
可视化二维嵌入向量空间
plt.figure(figsize=(8, 8))
plt.scatter(C[:, 0].data, C[:, 1].data, s=200)
for i in range(C.shape[0]):
plt.text(C[i, 0].item(), C[i, 1].item(), itos[i], ha="center", va="center", color="white")
plt.grid('minor')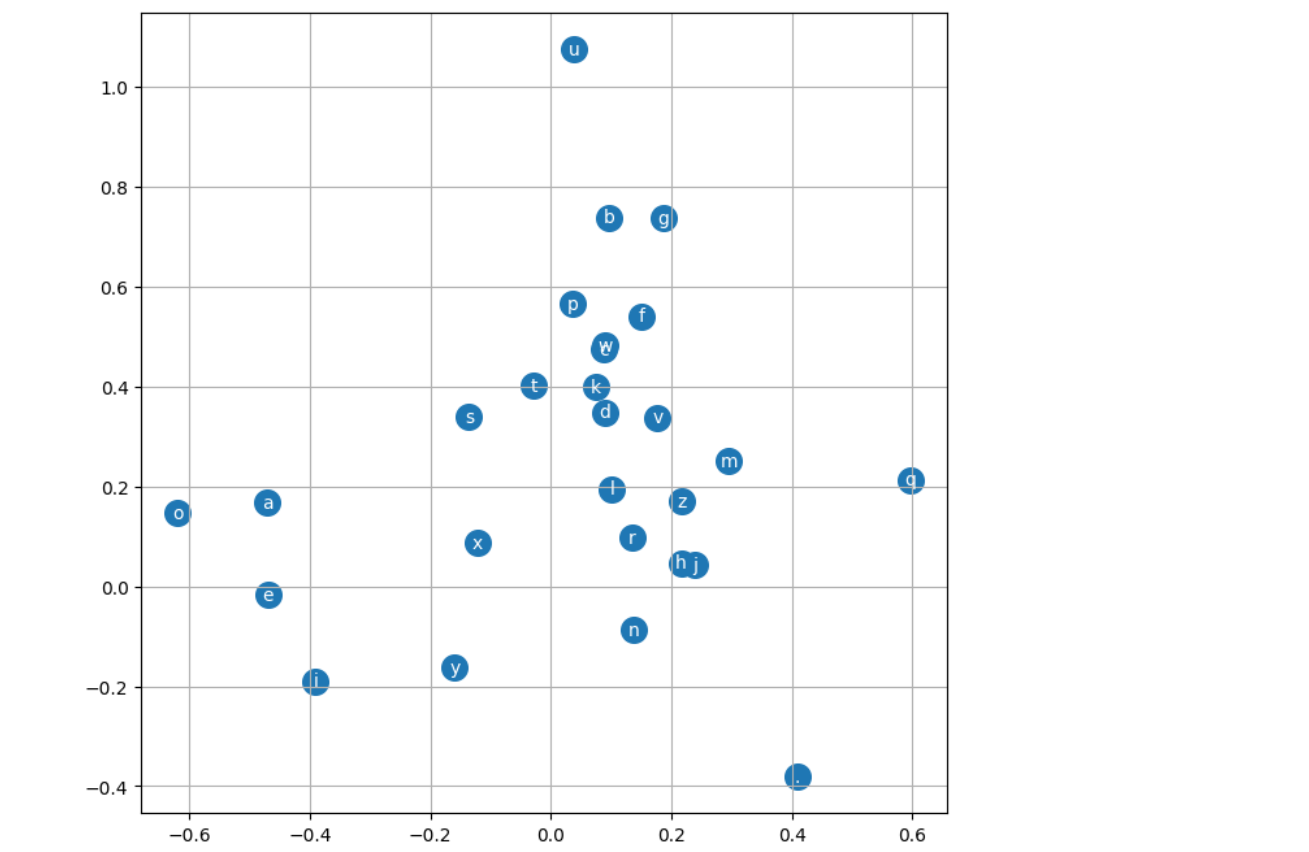
增加嵌入向量维度为 10
g = torch.Generator().manual_seed(xx)
C = torch.randn((27, 10), generator=g)
W1 = torch.randn((30, 300), generator=g) # 30 个输入进入隐藏层
b1 = torch.randn(300, generator=g)
W2 = torch.randn((300, 27), generator=g)
b2 = torch.randn(27, generator=g)
# 且修改, 对数化损失值
lossi.append(loss.log10().item())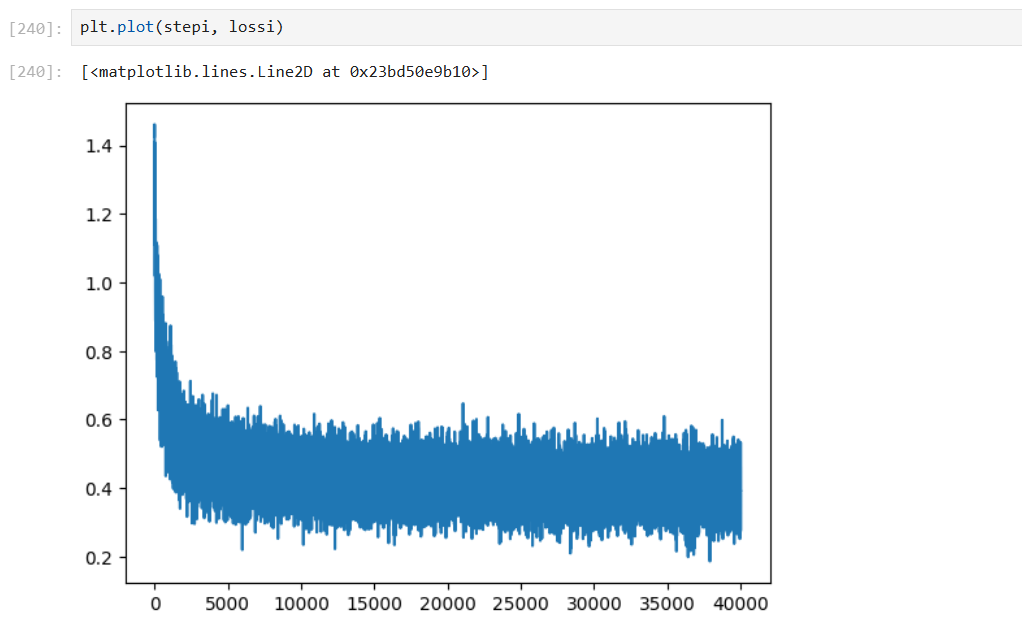
使用 0.01 为学习率后
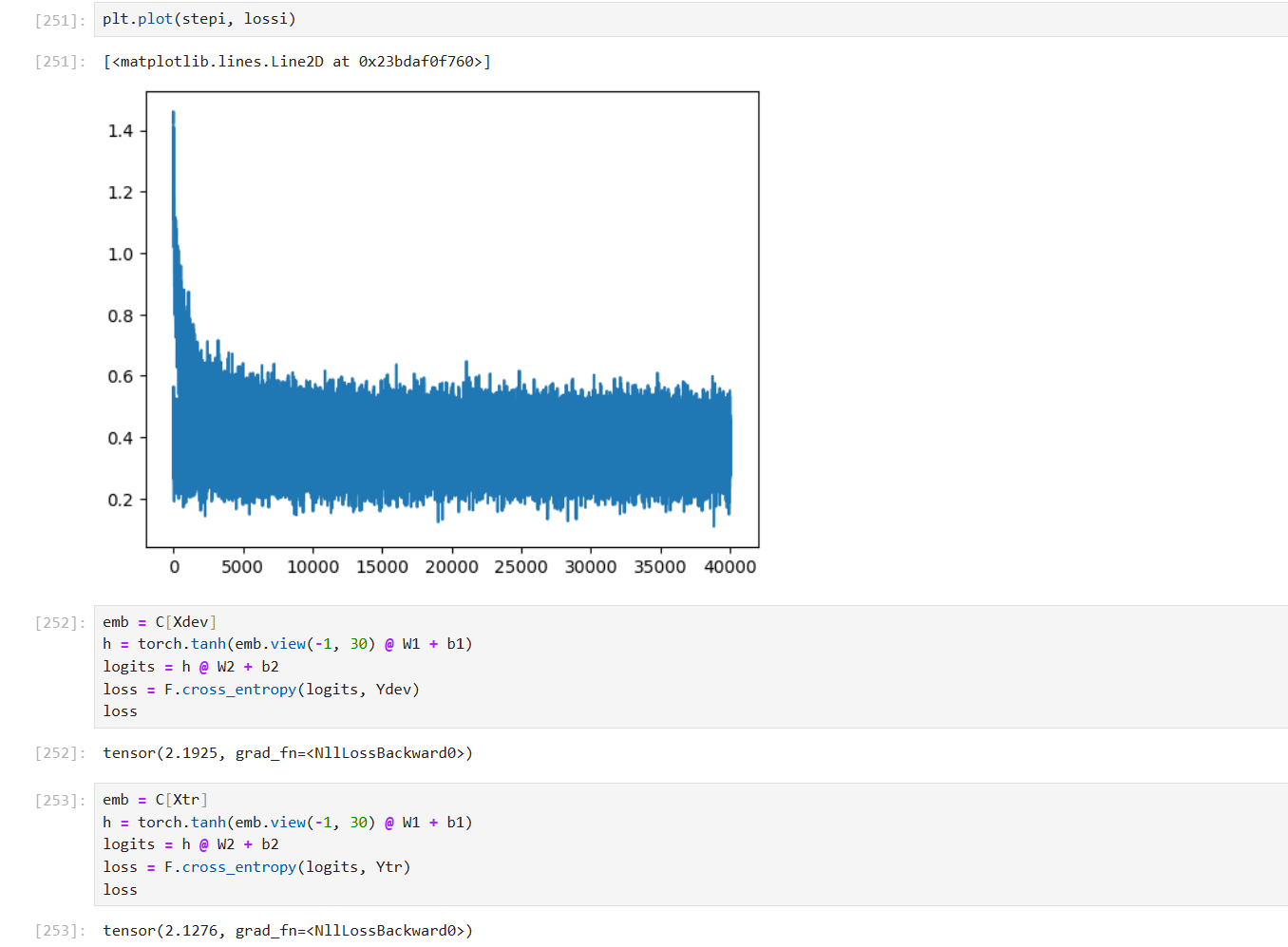
采样模型结果
# 通过模型采样
g = torch.Generator().manual_seed(2147483647 + 10)
for _ in range(20):
out = []
context = [0] * block_size
while True:
# 上下文字符索引转换为嵌入向量, 只处理一个样本
# 批量大小 1,上下文长度 block_size,嵌入维度 d
emb = C[torch.tensor([context])] # (1, block_size, d)
h = torch.tanh(emb.view(1, -1) @ W1 + b1) # 将嵌入展平为 (1, block_size*d)
logits = h @ W2 + b2
probs = F.softmax(logits, dim=1)
ix = torch.multinomial(probs, num_samples=1, generator=g).item()
context = context[1:] + [ix]
out.append(ix)
if ix == 0:
break
print(''.join(itos[i] for i in out))MLP Multilayer Perceptron Optimize
- 基于之前的 MLP 代码,将硬编码的参数移到外面可控制
缓解初始优化问题
- 由于第一次为随机初始化,第一次的损失很大,若以此实验为例,损失应该在
-torch.tensor(1/27.0).log()=3.29左右,应该每个字符的概率平均分布 - 于是希望网络初始化时对数概率
logits大致为 0,才能使得损失较小
对数概率来源:随机初始化的 W 权重矩阵和 b 偏置值
# 初始化时设置 W*0.01 或 W*0.1, b*0 使得接近 0, 减少第一次的损失值
W2 = torch.randn((n_hidden, vocab_size), generator=g) * 0.01
b2 = torch.randn(vocab_size, generator=g) * 0隐藏层处理-梯度消失
- 运行一次后查看隐藏层 h,经过
tanh后数据压缩在[-1, 1]中,其中 -1 和 1 的含量最高
plt.hist(h.view(-1).tolist(), 50) # 展平后转换为 python 列表, 构建直方图
# 柱子数量为 50, 统计每个数值区间的频数并绘制
plt.hist(hpreact.view(-1).tolist(), 50)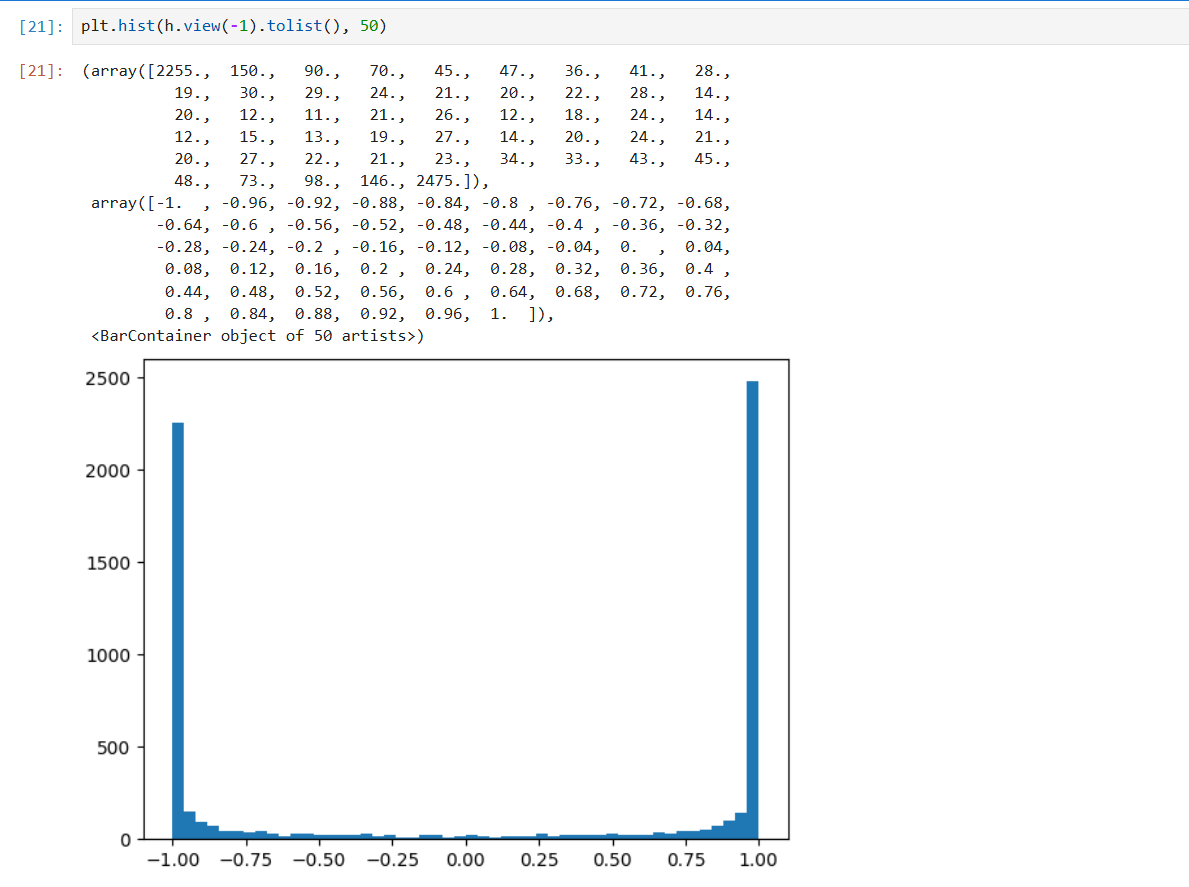
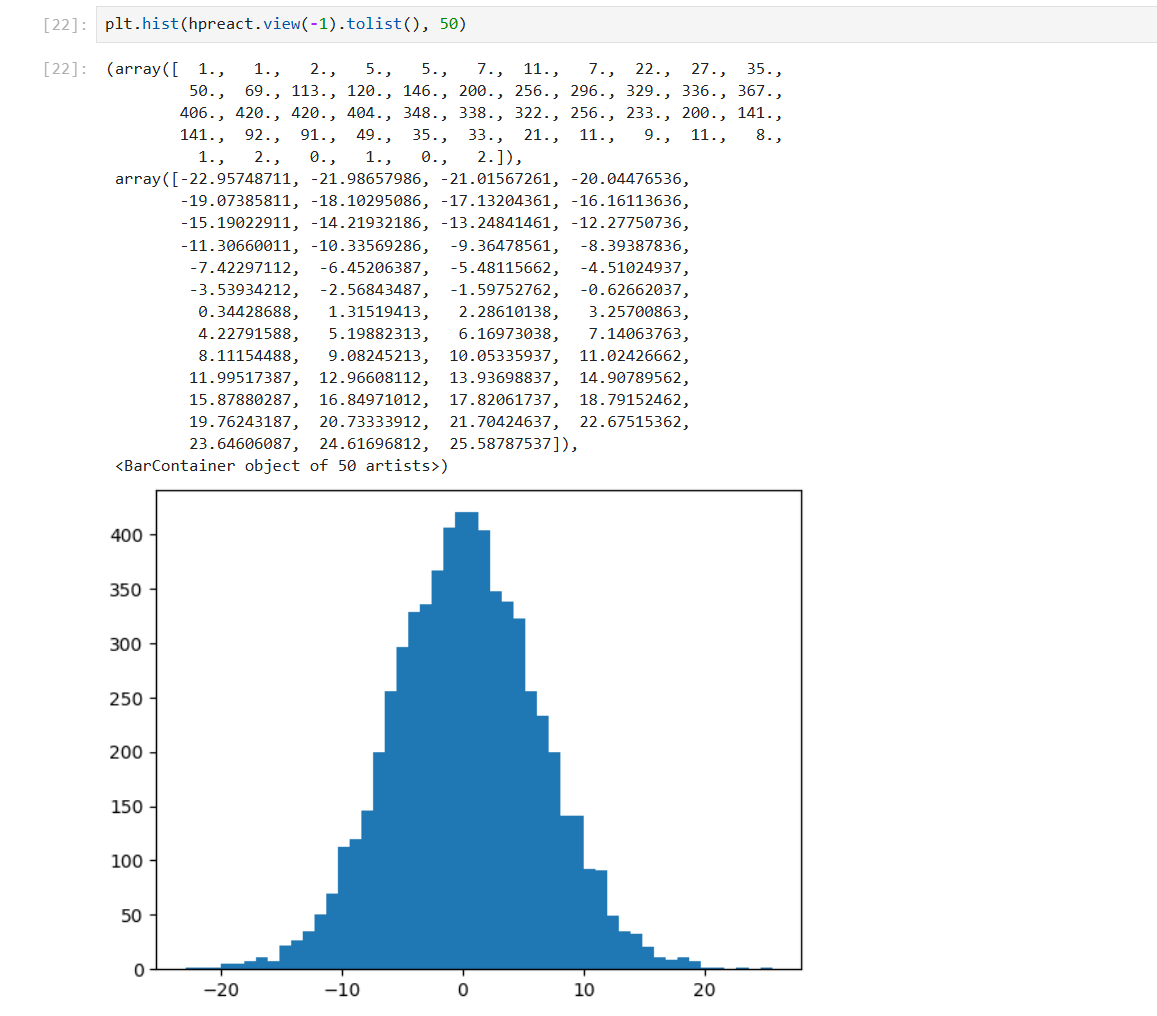
梯度消失
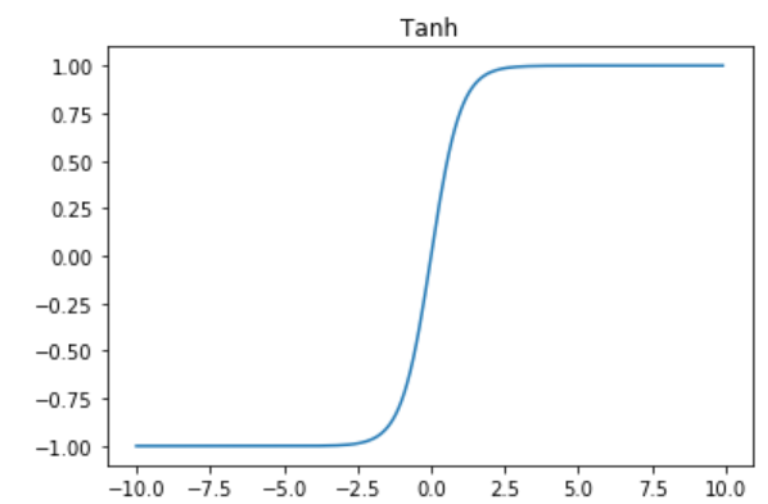
tanh 导数公式:tanh'(x) = 1 - tanh(x)²
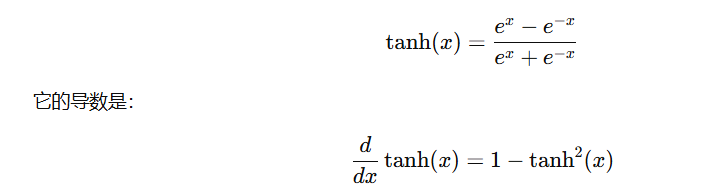
① tanh(x) ≈ 1 或 ≈ -1(平坦区)
- 对于 tanh 函数,输入很大时,输出非常接近 1 或 -1,即处于平坦区域,基本改变输入不会对 tanh 的输出产生太大影响,无论如何改变,损失都不会被影响
- 此时导数实际上接近或为 0
- 对于反向传播影响:
- 反向传播时,梯度乘上一个接近 0 的数,导致梯度消失
- 梯度为 0,权重无法有效更新,阻止了反向传播,停止学习
② tanh(x) = 0(激活的中心区域)
- tanh 输出为 0,代入导数得到 1
- 对反向传播影响:
- 反向梯度 = 外部梯度 × 1,梯度直接传递
- **梯度完全通过,没有衰减,没有放大,**对权重更新完全有贡献
plt.figure(figsize=(20,10))
plt.imshow(h.abs() > 0.99, cmap='gray', interpolation='nearest') # 查看平坦区比例, 真为白色, 假为黑色
若有完整的一列全白,则说明该层神经元为死神经元,梯度为 0,不会进行学习,无论从数据集输入什么,都会输出完全+1或完全-1
对于 sigmoid,ReLu 函数也同理,因为他们均是压缩函数,当小于 0 时,ReLu 关闭,梯度消失,大于 0 时通过
需要将 hpreact 变得倾向于 0,需要初始化将 W*0.1,将 b*0.01 使得接近 0,均值为 0 的高斯分布
W1 = torch.randn((n_embd * block_size, n_hidden), generator=g) * 0.1
b1 = torch.randn(n_hidden, generator=g) * 0.01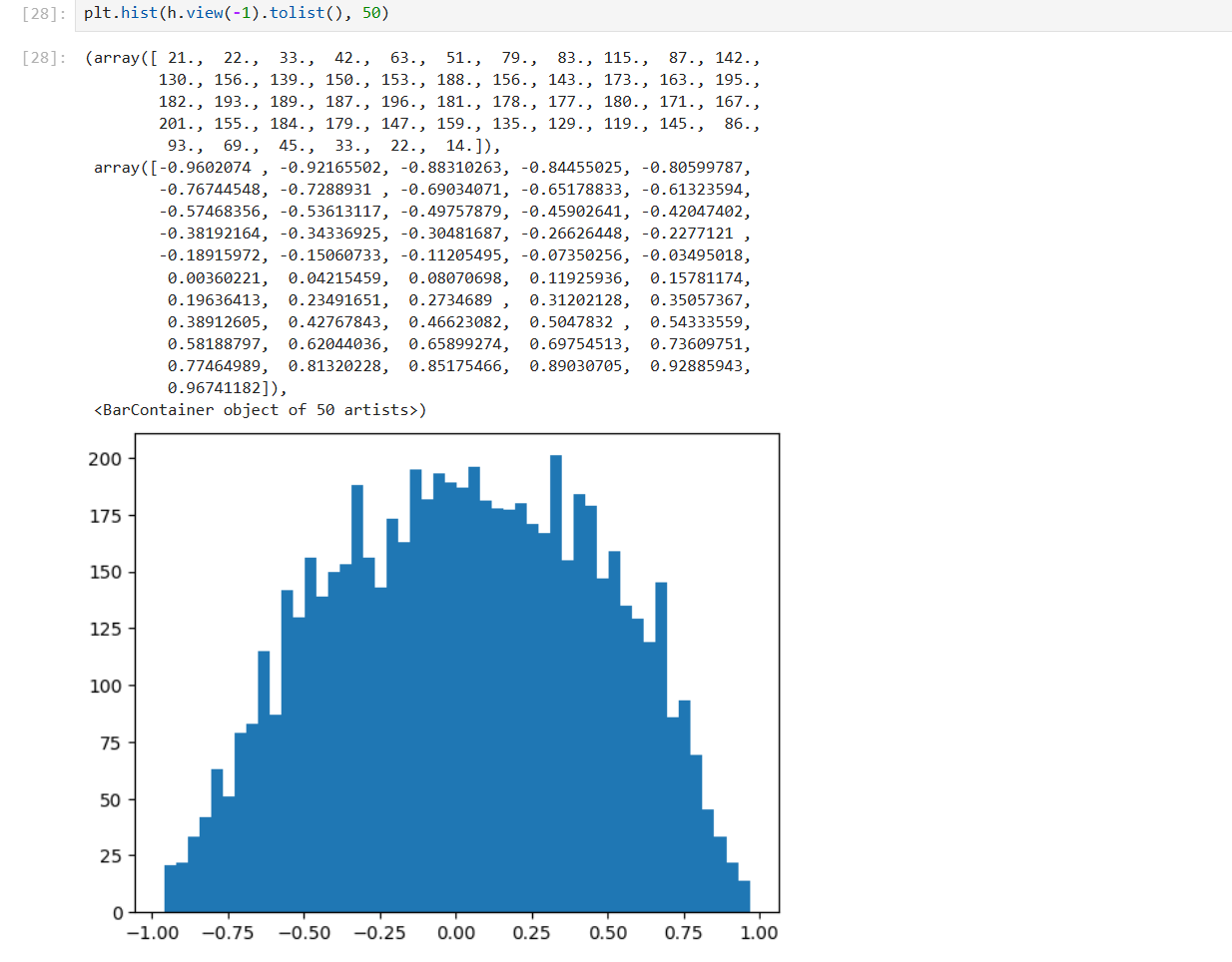

W1 = torch.randn((n_embd * block_size, n_hidden), generator=g) * 0.2
b1 = torch.randn(n_hidden, generator=g) * 0.01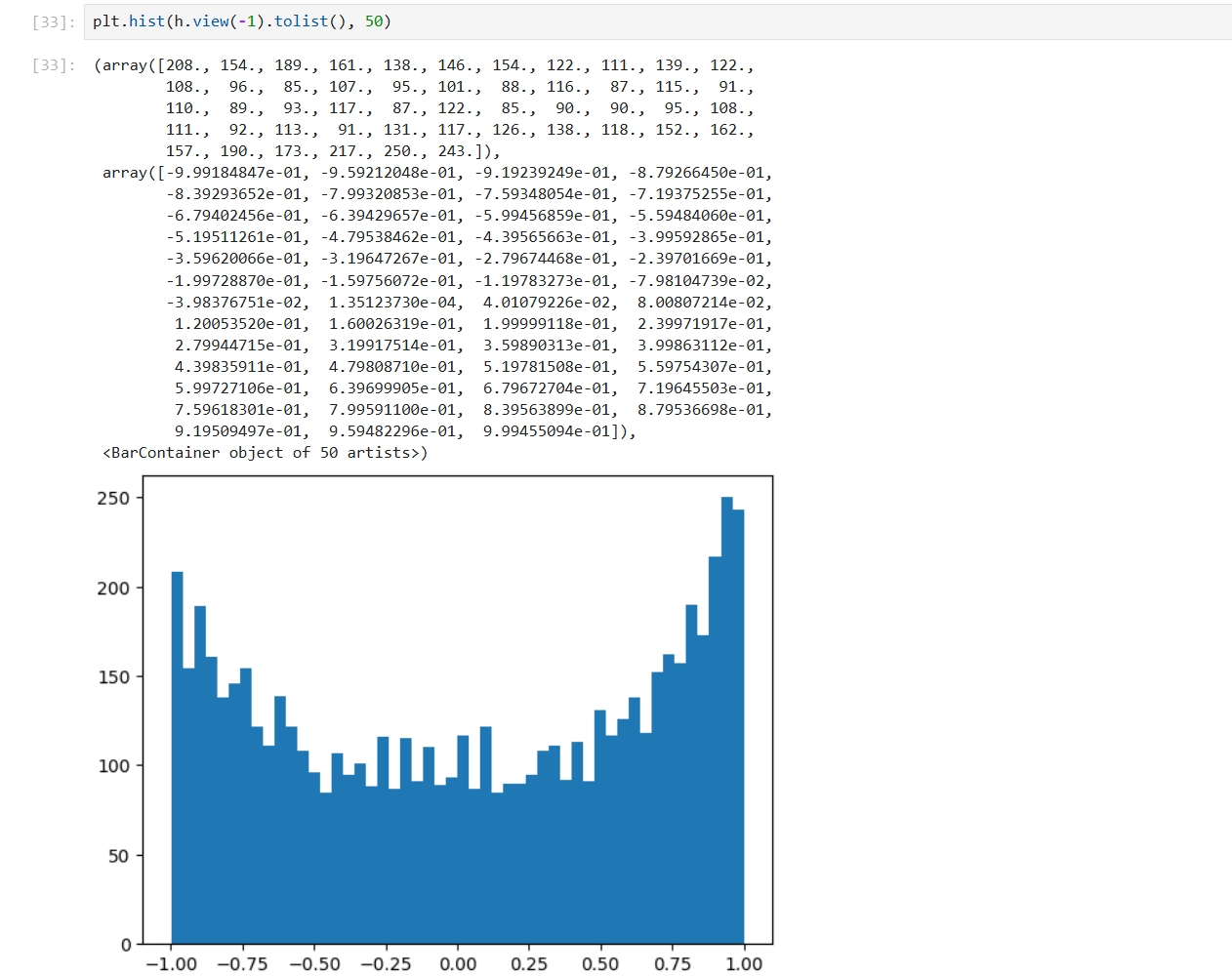

神经网络初始化
- 当神经网络层数增加时,希望确保激活函数表现良好,不会无限扩大或缩小到 0
当 X 和 W 为高斯分布的矩阵时,Y 为两矩阵相乘,此时 Y 的标准差要扩大,大于 X 的标准差,均值几乎不变,而我们希望其标准差也近乎不变
X = torch.randn(1000, 10)
W = torch.randn(10, 200) # 需要在此基础上乘上一个值, 可以改变标准差缩小增大, / 10**0.5
# 基本上乘以多少后标准差为多少倍, 输入归一化
Y = X @ W
print(X.mean(), X.std())
print(Y.mean(), Y.std())
plt.figure(figsize=(20, 5))
plt.subplot(121)
plt.hist(X.view(-1).tolist(), 50, density=True);
plt.subplot(122)
plt.hist(Y.view(-1).tolist(), 50, density=True);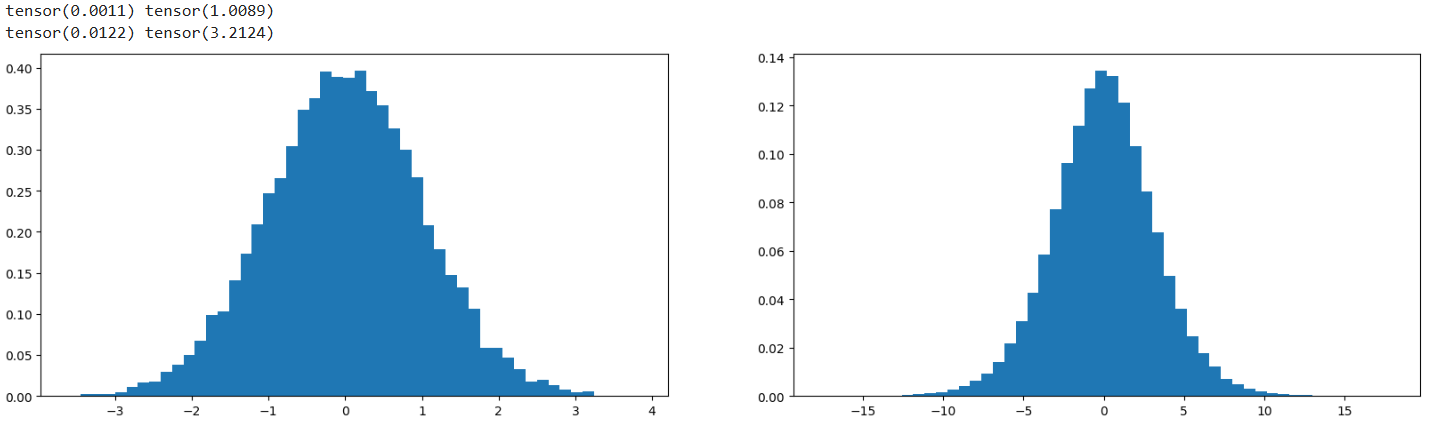
需要调整权重矩阵 W 来保持这种分布仍然是高斯分布,通过除以【输入量的平方根】,可以保证
- 若不仅仅为线性层,需要加入激活函数,对于不同的函数,增益 gain 也不同
- ReLU:根号 2
- Sigmoid:1
- Linear:1
- Tanh:5/3
- SELU:3/4
即所需要的标准差为增益和输入量计算得来,但到现代来说,初始化网络这些没有那么重要了
批量归一化层
- 2015-google-batch normalization,使得训练非常深的神经网络变得非常可靠且有效
- 将隐藏层激活值,批量标准化为高斯分布
hpreact = embcat @ W1 + b1 # (32, 200)
hpreact.mean(0, keepdim=True).shape # 均值 (1,200)
hpreact.std(0, keepdim=True).shape # 标准差 (1, 200)标准化激活值
且这些公式均可微分,可以直接训练
# 精确为高斯分布, 标准正态分布
hpreact = (hpreact - hpreact.mean(0, keepdim=True)) / hpreact.std(0, keepdim=True)还需要引入一个额外组件,缩放和平移,使得分布可以缩放和偏移
bngain = torch.ones((1, n_hidden))
bnbias = torch.zeros((1, n_hidden))
parameters = [C, W1, b1, W2, b2, bngain, bnbias]
hpreact = bngain * (hpreact - hpreact.mean(0, keepdim=True)) / hpreact.std(0, keepdim=True) + bnbias- 初始时,bngain 为 1,bnbias 为 0,这个批次每个神经元的激活值恰好是单位高斯分布,无论输入分布如何,输出的每个神经元的激活值都是单位高斯分布
- 优化过程中,根据反向传播调整 bngain 和 bnbias
- 批量归一化会导致耦合批次样本,实际上引入噪声填充了样本,并正则化神经网络
- 人们试图使用其他不耦合批次样本的归一化技术:层归一化/实例归一化/组归一化等
均值和标准差
评估训练集和验证集中的损失,有两种方法来确定使用哪个标准差和均值
第一种方式:校准批量归一化统计数据
- 先估算完整个训练集的均值和标准差,再去计算训练集和测试集的损失(两阶段运行)
with torch.no_grad():
emb = C[Xtr]
embcat = emb.view(emb.shape[0], -1)
hpreact = embcat @ W1 + b1
# 一次性估计/计算整个训练集的均值和标准差
bnmean = hpreact.mean(0, keepdim=True)
bnstd = hpreact.std(0, keepdim=True)- 修改评估训练集和验证集的损失代码
hpreact = (hpreact - bnmean) / bnstd + bnbias第二种方式:实际论文中还引入了额外想法,直接动态更新标准差和均值(无需两阶段,消除显式校准阶段)
- 参数增加,且这些参数不属于梯度更新优化的部分,需要在训练过程中被侧边更新
bnmean_running = torch.zeros((1, n_hidden))
bnstd_running = torch.ones((1, n_hidden))- 前向传播中
hpreact = embcat @ W1 + b1 # (32, 200)
bnmeani = hpreact.mean(0, keepdim=True)
bnstdi = hpreact.std(0, keepdim=True)
hpreact = bngain * (hpreact - bnmeani) / bnstdi + bnbias
# 上述代码中 bnstdi 也可加入一个极小值 epsilon 防止 bnstdi 为 0, 默认 10 的 -5 次方
...
# 不使用梯度下降更新, 平滑均值方式更新
with torch.no_grad():
bnmean_running = 0.999 * bnmean_running + 0.001 * bnmeani
bnstd_running = 0.999 * bnstd_running + 0.001 * bnstdi- 修改评估训练集和验证集的损失代码
hpreact = (hpreact - bnmean_running) / bnstd_running + bnbias最终需要实现 bnmean_running 和 bnmean 计算的相似,bnstd_running 和 bnstd 计算的相似
偏置值处理
出现了偏置值在归一化中抵消的情况
# 原始线性变化
hpreact = embcat @ W1 + b1
# 批量归一化
hpreact_normalized = (hpreact - mean(hpreact)) / std(hpreact)由于 mean(embcat @ W1 + b1) = mean(embcat @ W1) + b1 ,代入后
([embcat @ W1 + b1] - mean([embcat @ W1 + b1])) / std([embcat @ W1 + b1])
([embcat @ W1] + [b1] - mean([embcat @ W1]) - [b1]) / std([embcat @ W1 + b1])
# 此处 b1 被抵消了,所以 b1 对最终输出没有影响,所以梯度也为 0而此时批量归一化有一个偏置值 bnbias,所以在包含乘法运算的层(线性层/卷积层)后,加入批量归一化层时,可以将偏置值 b1 直接删除,不再需要(如残差神经网络中,重复结构的块被称为瓶颈块
对于残差网络:多个【卷积层、批量归一化层、ReLU】,此时卷积层就可以设置 bias=False
总结
- 训练时使用批次的均值和标准差,且需要不断更新动态变化标准差和均值(running)
- 非训练时使用动态变化的均值和标准差(running)
以下作图制作了不同层在取不同值(-1, 1)的分布图来总结,未使用标准归一化层的效果
前向传播激活值的统计和分布直方图
反向传播梯度的统计和分布直方图
作为随机梯度下降一部分将要更新的权重的统计和分布直方图
观察均值、标准差、梯度与数据的比例、更新量与数据的比例- 增益变化会使得每一层输出值的标准差及接近1的饱和度变化,对于 tanh 函数压缩分布,需要增益来缓解抵消该压缩
- 增益为 5/3 时,层数往后,标准差在 1 附近,饱和度从 20% 下降到 5% 左右
- 增益为 1 时,层数往后,标准差不断减小,从 0.6 减少到 0.3,饱和度从 3% 下降到 0%
- 增益变化会使得每一层梯度的标准差及接近1的饱和度变化,对于 tanh 函数
- 增益为 5/3 时,每层均值均为 0 附近,标准差在 3-4 之间
- 增益为 0.5 时,每层均值均为 0 附近,标准差差距变大
- 增益为 3 时,每层均值均为 0 附近,标准差出现不对称性
- 若移除 tanh 函数,仅仅为线性层,而增益仍为 5/3
- 输出的分布随着层数增加,开始变得分散
- 梯度的分布相反,随着层数增加,开始变得紧密
- 修改增益为 1 时,两者的分布基本相同,表现良好,不会随着层数增加改变太多
- 也可通过画图查看随着迭代次数,每次更新量的值变化,可以证明出学习率的高低
- 若初始线性层未使用输入归一化,可能会导致更新量的值震荡
使用归一化层放置于线性层和激活函数之间:
- 每一层的输出均值为 0,且标准差均在 0.64 附近
- 梯度和权重的分布也很好,可以改变增益、输入归一化增益的值来调整查看效果
Implementing backward propagation
- 作为练习手动实现反向传播机制
- 基于之前的模板,实现
loss.backward()
初始化
基础变化为
# 参数初始化阶段 仍使用 b1
# bngain = torch.ones((1, n_hidden))
# bnbias = torch.zeros((1, n_hidden))
bngain = torch.randn((1, n_hidden))*0.1 + 1.0
bnbias = torch.randn((1, n_hidden))*0.1
# bnmean_running = torch.zeros((1, n_hidden))
# bnstd_running = torch.ones((1, n_hidden))
# 小批量提出作为单独单元格
batch_size = 32
n = batch_size
ix = torch.randint(0, Xtr.shape[0], (batch_size, ), generator=g)
Xb, Yb = Xtr[ix], Ytr[ix]比较梯度函数
# 比较梯度工具
def cmp(s, dt, t):
ex = torch.all(dt == t.grad).item() # 比较完全一致
app = torch.allclose(dt, t.grad) # 浮点数上大致一致
maxdiff = (dt - t.grad).abs().max().item() # 最大差异
print(f'{s:15s} | exact: {str(ex):5s} | approximate: {str(app):5s} | maxdiff: {maxdiff}')主要部分
# 前向传播
emb = C[Xb] # 小批量
embcat = emb.view(emb.shape[0], -1) # 嵌入向量展平, 准备输入到全连接层
# 线性层 1
hprebn = embcat @ W1 + b1
# 归一化层
bnmeani = 1/n*hprebn.sum(0, keepdim=True) # 计算当前批次均值
bndiff = hprebn - bnmeani # 每个激活值与均值的差值
bndiff2 = bndiff**2 # 差值平方
bnvar = 1/(n-1)*(bndiff2).sum(0, keepdim=True) # 当前批次方差(无偏估计, 除以 n-1)
# 原论文奇怪的点: 训练时使用偏差估计, 测试时使用无偏估计
bnvar_inv = (bnvar + 1e-5)**-0.5 # 标准差的倒数(小常量防止除零)
bnraw = bndiff * bnvar_inv # 激活值归一化处理, 减去均值除以标准差
hpreact = bngain * bnraw + bnbias # 应用可学习的缩放和偏移参数
# 非线性层
h = torch.tanh(hpreact)
# 线性层 2
logits = h @ W2 + b2
# 损失计算
logit_maxes = logits.max(1, keepdim=True).values # 每个样本最大 logit 值
norm_logits = logits - logit_maxes # 所有 logits 中减去最大值, 防止指数运算溢出
counts = norm_logits.exp() # 计算指数得到未归一化的概率
counts_sum = counts.sum(1, keepdim=True) # 计算每个样本概率总和, 归一化
counts_sum_inv = counts_sum**-1 # 计算总和的倒数, 计算 softmax 概率
probs = counts * counts_sum_inv # 每个 count 除以总和, 计算 softmax 概率
logprobs = probs.log() # 计算概率对数
loss = -logprobs[range(n), Yb].mean()
# 选择了每个样本真实正确类别对应的对数概率,计算交叉熵损失
# pytorch 反向传播
for p in parameters:
p.grad = None
for t in [logprobs, probs, counts, counts_sum, counts_sum_inv,
norm_logits, logit_maxes, logits, h, hpreact, bnraw,
bnvar_inv, bnvar, bndiff2, bndiff, hprebn, bnmeani,
embcat, emb]:
t.retain_grad()
loss.backward() # 执行反向传播,计算所有参数的梯度
loss反向传播实现
dxxx 计算损失相对于 xxx 的导数, shape 相同
dlogprobs - loss:logprobs
# loss 简化
loss = (a + b + ... + y) / n # n 为 32, 括号内 32 个数
dloss / da = -1/n # 实际对于 32 个值里任何一个都是 -1/32
# logprobs: (32, 27), 除了对应 32 个值外其余的值实际对 loss 无影响, 梯度为 0
dlogprobs = torch.zeros_like(logprobs)
dlogprobs[range(n), Yb] = -1.0/n # 设置对应的 32 个梯度
cmp('logprobs', dlogprobs, logprobs)
# logprobs | exact: True | approximate: True | maxdiff: 0.0dprobs - logprobs:probs
# logx 导数 1/x
dprobs = (1.0 / probs) * dlogprobs # 链式法则
cmp('probs', dprobs, probs)
# probs | exact: True | approximate: True | maxdiff: 0.0dcounts_sum_inv - probs:counts_sum_inv
probs = counts * counts_sum_inv # counts(32, 27), counts_sum_inv(32, 1)
# 简化
c = a * b
a[3x3] * b[3,1] ->
a11*b1 a12*b1 a13*b1
a21*b2 a22*b2 a23*b2
a31*b3 a32*b3 a33*b3
c[3x3] # 乘法求导 dc/db = a
# 通过 sum 来处理重复的 b
dcounts_sum_inv = (counts * dprobs).sum(1, keepdim=True) # (32, 1)
cmp('counts_sum_inv', dcounts_sum_inv, counts_sum_inv)
# counts_sum_inv | exact: True | approximate: True | maxdiff: 0.0dcounts - probs:counts
# 乘法求导 dc/da = b
dcounts = counts_sum_inv * dprobs # (32, 1) * (32, 27) -> (32, 27)dcounts_sum - counts_sum_inv:counts_sum
# 1/x 导数 -1/(x^2)
dcounts_sum = (-counts_sum**-2) * dcounts_sum_inv # (32, 1)
cmp('counts_sum', dcounts_sum, counts_sum)
# counts_sum | exact: True | approximate: True | maxdiff: 0.0dcounts - counts_sum:counts
# 对于 counts_sum = counts.sum(1, keepdim=True) 沿着行的总和
# counts_sum (32, 1) counts (32, 27)
# a11 a12 a13 ----> b1 (= a11 + a12 + a13)
# a21 a22 a23 ----> b2 (= a21 + a22 + a23)
# a31 a32 a33 ----> b3 (= a31 + a32 + a33)
# 导数均匀分配 db1/da11 = 1, db1/da12 = 1, db1/da13 = 1, 而b1 对第二三行所有元素导数为 0
dcounts += torch.ones_like(counts) * dcounts_sum # dcounts 由不同计算影响相加获取
cmp('counts', dcounts, counts)
# counts | exact: True | approximate: True | maxdiff: 0.0dnorm_logits - counts:norm_logits
# counts = norm_logits.exp() e^x 导数为 e^x
dnorm_logits = counts * dcounts # counts 即为 norm_logits.exp()
cmp('norm_logits', dnorm_logits, norm_logits)
# norm_logits | exact: True | approximate: True | maxdiff: 0.0dlogits - norm_logits:logits
# norm_logits (32, 27), logits (32, 27) logit_maxes (32, 1)
# c11 c12 c13 = a11 a12 a13 b1
# c21 c22 c23 = a21 a22 a23 - b2
# c31 c32 c33 = a31 a32 a33 b3
# c32 = a32 - b3
dlogits = dnorm_logits.clone() # *1
# dlogits 还未结束, 来源于 norm_logits 和 logit_maxesdlogit_maxes - norm_logits:logit_maxes
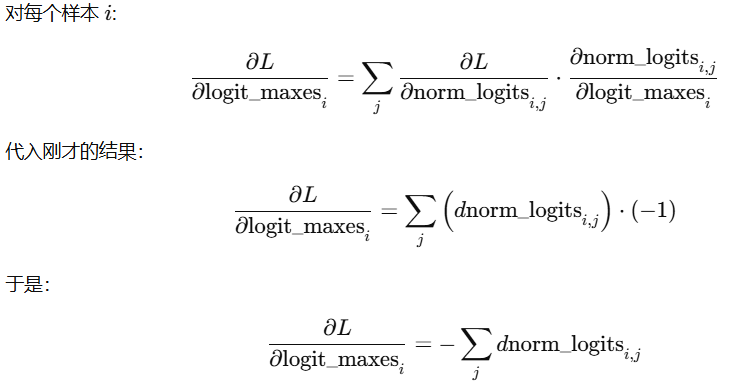
# norm_logits 是对 logits 的 平移操作:把每行整体减去最大值
# 一个标量影响了整行向量 -> 它的梯度必须是这一行梯度的总和
# 因为 logit_maxes[i] 被广播复制到多个位置,每个位置产生的损失贡献都必须加回来
# 任何广播过的标量,其梯度都必须把它影响的所有位置累加回来
dlogit_maxes = (-dnorm_logits).sum(1, keepdim=True)
cmp('logit_maxes', dlogit_maxes, logit_maxes)
# logit_maxes | exact: True | approximate: True | maxdiff: 0.0dlogits - logit_maxes:logits
对于 logits 的每一行,若对所有元素加上或减少相同的值,probs 的值实际将保持不变,未改变 softmax,减去最大值的唯一目的是防止指数不会溢出,避免指数爆炸,max 目的保证 logits 每一行最大值为 0

# logit_maxes = logits.max(1, keepdim=True).values 每行取出最大值所在索引的值(索引不同)
# 热编码解决,对应的值为 1, 直接传递 dlogit_maxes
dlogits += F.one_hot(logits.max(1).indices, num_classes=logits.shape[1]) * dlogit_maxes
cmp('logits', dlogits, logits)
# logits | exact: True | approximate: True | maxdiff: 0.0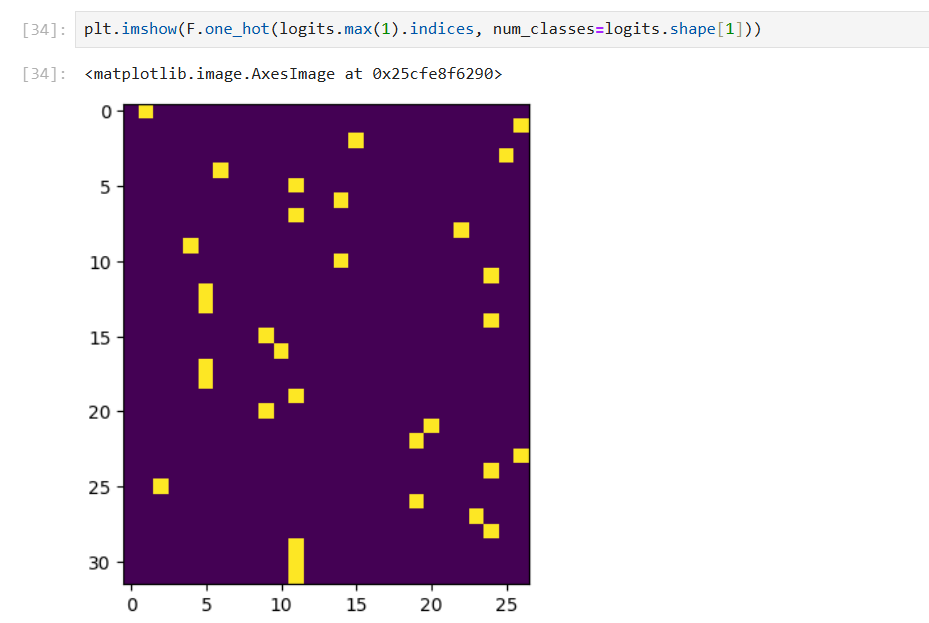
dh - logits:h
dW2 - logits:W2
db2 - logits:b2
# logits = h @ W2 + b2
# dlogits (32, 27) h (32, 64) W2 (64, 27) b2 (27)
dh = dlogits @ W2.T
dW2 = h.T @ dlogits
db2 = dlogits.sum(0)
cmp('h', dh, h)
cmp('W2', dW2, W2)
cmp('b2', db2, b2)
# h | exact: True | approximate: True | maxdiff: 0.0
# W2 | exact: True | approximate: True | maxdiff: 0.0
# b2 | exact: True | approximate: True | maxdiff: 0.0推导过程
d = a @ b + c
d11 d12 a11 a12 b11 b12 c1 c2
d21 d22 = a21 a22 * b21 b22 + c1 c2
# 即
d11 = a11b11 + a12b21 + c1
d12 = a11b12 + a12b22 + c2
d21 = a21b11 + a22b21 + c1
d22 = a21b12 + a22b22 + c2
dL/da11 = dL/dd11 * b11 + dL/dd12 * b12
dL/da12 = dL/dd11 * b21 + dL/dd12 * b22
dL/da21 = dL/dd21 * b11 + dL/dd22 * b12
dL/da22 = dL/dd21 * b21 + dL/dd22 * b22
dL/da11 dL/da12 dL/dd11 dL/dd12 b11 b21
dL/da21 dL/da22 = dL/dd21 dL/dd22 * b12 b22 = dL/dd @ b^T
# 最终
dL/da = dL/dd @ b^T
dL/dc = dL/dd * sum(0)
dL/db = a^T @ dL/dddhpreact - h:hpreact
# h = torch.tanh(hpreact)
dhpreact = (1.0 - h**2) * dh
cmp('hpreact', dhpreact, hpreact)
# hpreact | exact: True | approximate: True | maxdiff: 0.0dbngain - hpreact:bngain
dbnraw - hpreact:bnraw
dbnbias - hpreact:bnbias
# hpreact (32, 64) bngain (1, 64) bnraw (32, 64) bnbias (1, 64)
# hpreact = bngain * bnraw + bnbias
dbngain = (bnraw * dhpreact).sum(0, keepdim=True) # (32, 64) -> (1, 64)
dbnraw = bngain * dhpreact
dbnbias = dhpreact.sum(0, keepdim=True) # (32, 64) -> (1, 64)
cmp('bngain', dbngain, bngain)
cmp('bnraw', dbnraw, bnraw)
cmp('bnbias', dbnbias, bnbias)
# bngain | exact: True | approximate: True | maxdiff: 0.0
# bnraw | exact: True | approximate: True | maxdiff: 0.0
# bnbias | exact: True | approximate: True | maxdiff: 0.0dbnvar_inv - bnraw:bnvar_inv
dbndiff - bnraw:bndiff
# bnraw = bndiff * bnvar_inv
# bnraw (32, 64) bndiff (32, 64) bnvar_inv (1, 64)
dbndiff = bnvar_inv * dbnraw
dbnvar_inv = (bndiff *dbnraw).sum(0, keepdim=True)
cmp('bnvar_inv', dbnvar_inv, bnvar_inv)
# bnvar_inv | exact: True | approximate: True | maxdiff: 0.0dbnvar - bnvar_inv:bnvar
# bnvar_inv = (bnvar + 1e-5)**-0.5
dbnvar = (-0.5*(bnvar + 1e-5)**-1.5) * dbnvar_inv
cmp('bnvar', dbnvar, bnvar)
# bnvar | exact: True | approximate: True | maxdiff: 0.0dbndiff2 - bnvar:bndiff2
总结:前向传播有求和时,反向传播变成沿着同一维度复制或广播;前向传播中有复制或广播时,反向传播变成对同一维度的求和
# bnvar = 1/(n-1)*(bndiff2).sum(0, keepdim=True)
# bnvar (1, 64) bndiff2 (32, 64)
dbndiff2 = (1.0/(n-1))*torch.ones_like(bndiff2)*dbnvar # (32,64) * (1, 64) -> (32, 64)
cmp('bndiff2', dbndiff2, bndiff2)
# bndiff2 | exact: True | approximate: True | maxdiff: 0.0dbndiff - bndiff2:bndiff
# bndiff2 = bndiff**2
dbndiff += (2*bndiff) * dbndiff2
cmp('bndiff', dbndiff, bndiff)
# bndiff | exact: True | approximate: True | maxdiff: 0.0dbnmeani - bndiff:bnmeani
dhprebn - bndiff:hprebn
# bndiff = hprebn - bnmeani
# bndiff (32, 64) hprebn (32, 64) bnmeani (1, 64)
dhprebn = dbndiff.clone()
dbnmeani = (-torch.ones_like(bndiff) * dbndiff).sum(0)
cmp('bnmeani', dbnmeani, bnmeani)
# bnmeani | exact: True | approximate: True | maxdiff: 0.0dhprebn - bnmeani:hprebn
# bnmeani = 1/n * hprebn.sum(0, keepdim=True)
dhprebn += 1.0/n * (torch.ones_like(hprebn) * dbnmeani)
cmp('hprebn', dhprebn, hprebn)
# hprebn | exact: True | approximate: True | maxdiff: 0.0dembcat - hprebn:embcat
dW1 - hprebn:W1
db1 - hprebn:b1
# hprebn (32, 64) embcat (32, 30) W1 (30, 64) b1 (64)
dembcat = dhprebn @ W1.T
dW1 = embcat.T @ dhprebn
db1 = dhprebn.sum(0)
cmp('embcat', dembcat, embcat)
cmp('W1', dW1, W1)
cmp('b1', db1, b1)
# embcat | exact: True | approximate: True | maxdiff: 0.0
# W1 | exact: True | approximate: True | maxdiff: 0.0
# b1 | exact: True | approximate: True | maxdiff: 0.0demb - embcat:emb
# embcat = emb.view(emb.shape[0], -1)
# embcat (32, 30) emb (32, 3, 10)
demb = dembcat.view(emb.shape)
cmp('emb', demb, emb)
# emb | exact: True | approximate: True | maxdiff: 0.0dC - emb:C
# emb = C[Xb]
# emb (32, 3, 10) C (27, 10) Xb (32, 3)
dC = torch.zeros_like(C)
for k in range(Xb.shape[0]): # 32
for j in range(Xb.shape[1]): # 3
ix = Xb[k,j] # 获取索引
dC[ix] += demb[k, j] # 累加梯度, 同一个C的行可能被多个Xb位置使用, 所以梯度要累加
cmp('C', dC, C)
# C | exact: True | approximate: True | maxdiff: 0.0Building a WaveNet
基础环境复用
- 希望更多序列中字符输入,deepmind 2016 年 wavenet,语言模型预测音频序列,自回归模型
- 复用先前到训练集验证集划分的代码
模块化构建:线性层、标准化归一层、激活函数
# 线性层
class Linear:
def __init__(self, fan_in, fan_out, bias=True):
self.weight = torch.randn((fan_in, fan_out)) / fan_in**0.5 # note: kaiming init
self.bias = torch.zeros(fan_out) if bias else None
def __call__(self, x):
self.out = x @ self.weight
if self.bias is not None:
self.out += self.bias
return self.out
def parameters(self):
return [self.weight] + ([] if self.bias is None else [self.bias])
class Tanh:
def __call__(self, x):
self.out = torch.tanh(x)
return self.out
def parameters(self):
return []调整批量归一化
- ndim 维度数量为 2:在批次维度上计算均值和方差
- ndim 维度数量为 3:在批次维度和序列维度上计算均值和方差
# 标准化归一层
class BatchNorm1d:
def __init__(self, dim, eps=1e-5, momentum=0.1):
self.eps = eps
self.momentum = momentum
self.training = True
# parameters (trained with backprop)
self.gamma = torch.ones(dim)
self.beta = torch.zeros(dim)
# buffers (trained with a running 'momentum update')
self.running_mean = torch.zeros(dim)
self.running_var = torch.ones(dim)
def __call__(self, x):
# calculate the forward pass
if self.training:
##################### 添加 ###############################
#
if x.ndim == 2:
dim = 0
elif x.ndim == 3:
dim = (0,1)
xmean = x.mean(dim, keepdim=True) # batch mean
xvar = x.var(dim, keepdim=True) # batch variance
##################### 添加 ###############################
else:
xmean = self.running_mean
xvar = self.running_var
xhat = (x - xmean) / torch.sqrt(xvar + self.eps) # normalize to unit variance
self.out = self.gamma * xhat + self.beta
# update the buffers
if self.training:
with torch.no_grad():
self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * xmean
self.running_var = (1 - self.momentum) * self.running_var + self.momentum * xvar
return self.out
def parameters(self):
return [self.gamma, self.beta]初始化生成器:torch.manual_seed(xx)
n_embd = 10
n_hidden = 200
C = torch.randn((vocab_size, n_embd))
layers = [
Linear(n_embd * block_size, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(),
Linear(n_hidden, vocab_size),
]
# 参数初始化
parameters = [C] + [p for layer in layers for p in layer.parameters()]
print(sum(p.nelement() for p in parameters))
for p in parameters:
p.requires_grad = True前向传播修改
# 前向传播
emb = C[Xb] # 只获取 32 行 (32, 3, 2)
x = emb.view(emb.shape[0], -1)
for layer in layers:
x = layer(x)
loss = F.cross_entropy(x, Yb)训练完成后
for layer in layers:
layer.training = False # 设置为 False 控制标准归一化层优化 lossi 图像
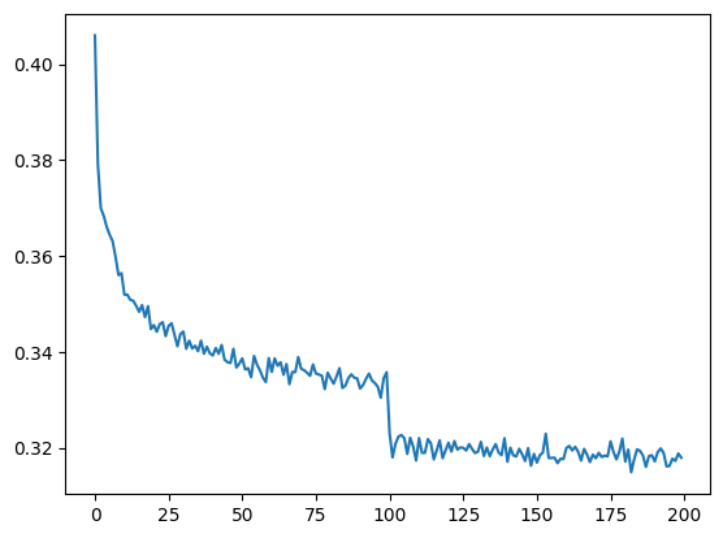
# old: plt.plot(lossi)
# 由于不断震荡,尝试将多组组成一个平均值优化
plt.plot(torch.tensor(lossi).view(-1, 1000).mean(1)) # 每 1000 个算平均值可以观察到学习率衰减
模块添加
加入嵌入模块和分块模块,分别执行索引和分块操作
# 嵌入层
class Embedding:
def __init__(self, num_embeddings, embedding_dim):
self.weight = torch.randn((num_embeddings, embedding_dim))
def __call__(self, IX):
self.out = self.weight[IX]
return self.out
def parameters(self):
return [self.weight]
# 扁平层
class Flatten:
def __call__(self, x):
self.out = x.view(x.shape[0], -1)
return self.out
def parameters(self):
return []修改代码
# C = torch.randn((vocab_size, n_embd)) 删除 C
layers = [
Embedding(vocab_size, n_embd),
Flatten(),
Linear(n_embd * block_size, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(),
Linear(n_hidden, vocab_size),
]
# 前向传播中
# emb = C[Xb] # 删除
# x = emb.view(emb.shape[0], -1) # 删除
x = Xb
for layer in layers:
x = layer(x)加入容器,定义模型概念
class Sequential:
def __init__(self, layers):
self.layers = layers
def __call__(self, x):
for layer in self.layers:
x = layer(x)
self.out = x
return self.out
def parameters(self):
# get parameters of all layers and stretch them out into one list
return [p for layer in self.layers for p in layer.parameters()]修改代码
model = Sequential([
Embedding(vocab_size, n_embd),
Flatten(),
Linear(n_embd * block_size, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(),
Linear(n_hidden, vocab_size),
])
parameters = model.parameters() # 获取参数
# 前向传播
logits = model(Xb)
loss = F.cross_entropy(logits, Yb)
for layer in model.layers:
layer.training = False # 关键, 批量归一化层是否是训练模式
# 训练集验证集损失
logits = model(x)
# 通过模型采样
logits = model(torch.tensor([context]))连续扁平层实现
- 预测下一个字符,不是前面所有不同字符压缩,而是取两个字符慢慢压缩,因果扩张卷积可视化
- 加深层数,但只取两个字符,接着 2 个二元语法,接着 2 个四元语法
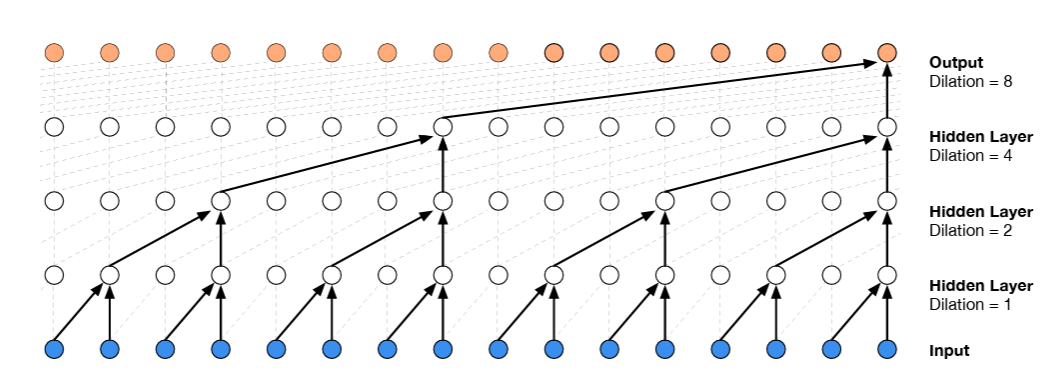
修改上下文块大小,8 字符预测第 9 个字符
block_size = 8 # 参数量增加了 10000此时正以过快速度压缩过多信息,损失比原先减小了
# 中间层查看
model.layers[ix].out.shape矩阵乘法只作用于输入张量的最后一个维度之前维度不变
(torch.randn(4, 5, 2, 80) @ torch.rand(80, 200) + torch.randn(200)).shape
# (4, 5, 2, 200)
# (1 2) (3 4) (5 6) (7 8) 并行处理二元组,两个一组的4个分组,每个 10 维向量- 各层形状
- 嵌入层输出:(4, 8, 10)
- 扁平层输出:(4, 80)
- 线性层输出:(4, 200)
(torch.randn(4, 80) @ torch.rand(80, 200) + torch.randn(200)).shape
# (4, 200)
# 想要实现
(torch.randn(4, 4, 20) @ torch.rand(20, 200) + torch.randn(200)).shape
# (4, 4, 200) 第一个4是第一个批量维度,第二个4是第二个批量维度(每个例子中4个分组) 获取偶数部分和奇数部分
list(range(10))[::2]
list(range(10))[1::2]实现 (4, 4, 20):连续的10维向量在第二维度被连接
e = torch.randn(4, 8, 10)
torch.cat([e[:, ::2, :], e[:, 1::2, :]], dim=2).shape # (4, 4, 20)连续扁平层
本质是用块状拼接来模拟卷积的感受野扩张
class FlattenConsecutive:
def __init__(self, n):
self.n = n # 指定要将多少个连续的时间步合并在一起
def __call__(self, x):
B, T, C = x.shape
# B: 批次大小, T: 序列长度, C: 特征通道数
x = x.view(B, T//self.n, C*self.n)
# 序列长度减少为原来的 1/n 特征维度增加为原来的 n 倍
if x.shape[1] == 1:
x = x.squeeze(1) # 展平后序列长度变为1,就移除该维度, 输出形状从 (B, 1, C*n) 变为 (B, C*n)
self.out = x
return self.out
def parameters(self):
return []
# 构造模型修改
FlattenConsecutive(block_size),查看模型层数
# 随机选择4个样本的索引
ix = torch.randint(0, Xtr.shape[0], (4, ))
Xb, Yb = Xtr[ix], Ytr[ix]
logits = model(Xb)
for layer in model.layers:
print(layer.__class__.__name__, ':', tuple(layer.out.shape))
# Embedding : (4, 8, 10) 4个样本, 每个样本8个字符索引, 每个字符索引转换为10维向量
# FlattenConsecutive : (4, 80) 扁平化
# Linear : (4, 200)
# BatchNorm1d : (4, 200)
# Tanh : (4, 200)
# Linear : (4, 27)增加模型:三层神经网络
# 其中的 block_size 减小到 2
model = Sequential([
Embedding(vocab_size, n_embd),
FlattenConsecutive(2), Linear(n_embd * 2, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(),
FlattenConsecutive(2), Linear(n_hidden * 2, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(),
FlattenConsecutive(2), Linear(n_hidden * 2, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(),
Linear(n_hidden, vocab_size),
])
# 参数量 170897
# 减少隐藏层 n_hidden
n_hidden = 68 # 参数量减少到 22397卷积:并行,高效循环,空间维度上高效地应用相同的线性变换
- 共享权重:同一个卷积核滑动
- 局部连接:每个输出位置只连接输入的局部区域
- 参数效率:无论输入多大,参数数量不变
Building GPT
GPT:generatively pre-trained transformer,生成式预训练转换器,基于 transformer 训练一个字符级别语言模型
- 使用数据集,文学作品集
初始模型构建
包导入
import torch
import torch.nn as nn
from torch.nn import functional as F
torch.manual_seed(1337)超参数
batch_size = 32 # 一次并行同时处理多少值, 每个批次 32 个样本
block_size = 8 # 上下文大小
# 1 2 3 4 5 6 7 8 9
# 示例: 1 的上下文中 2 是下一个
# 示例: 1,2 的上下文中 3 是下一个
# 示例: 1,2,3 的上下文中 4 是下一个
max_iters = 3000 # 训练迭代次数
eval_interval = 300 # 间隔输出
learning_rate = 1e-2 # 学习率
device = 'cuda' if torch.cuda.is_available() else 'cpu'
eval_iters = 200 # 评估迭代次数
# 新加入
n_embd = 32 # 嵌入向量数量读取数据集
with open('input.txt', 'r', encoding='utf-8') as f:
text = f.read()
print(len(text)) # 1115393
chars = sorted(list(set(text)))
vocab_size = len(chars)
print(''.join(chars)) # !$&',-.3:;?ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz
print(vocab_size) # 65构建编码器和解码器
- google 的 sentencepiece,openai 的 tiktoken
tiktoken.get_encoding('gpt2').n_vocab为 50257个 token
stoi = { ch:i for i,ch in enumerate(chars) }
itos = { i:ch for i,ch in enumerate(chars) }
encode = lambda s: [stoi[c] for c in s]
decode = lambda l: ''.join([itos[i] for i in l])
# 划分训练集和验证集
data = torch.tensor(encode(text), dtype=torch.long)
n = int(0.9*len(data))
train_data = data[:n]
val_data = data[n:]让 transformer 网络习惯于看到从最少一个到整个块大小的各种上下文,看到中间过程对于后续推理阶段阶段更有用,采样时,可从一个字符的上下文开始生成样本,transformer 预测下一个字符,超过块大小后必须截断,transformer 在预测下一个字符时永远不会接收到超过块大小的输入
从训练集或验证集中随机抽取指定数量的连续数据块作为训练批次
def get_batch(split):
data = train_data if split == 'train' else val_data
ix = torch.randint(len(data) - block_size, (batch_size, )) # ix 为 batch_size 个随机值
# 对每个随机索引 i, 从数据中截取长度为 block_size 的序列
# stack 前: [tensor([...]), tensor([...]), ...]
# stack 后: tensor([[...], [...], ...])
x = torch.stack([data[i:i+block_size] for i in ix])
y = torch.stack([data[i+1:i+block_size+1] for i in ix])
# y 中每个位置对应 x 中相应位置的下一个词元 token
x, y = x.to(device), y.to(device)
return x, y
# 用法: xb, yb = get_batch('train') shape: (batch_size, block_size) 即 (B, T)**损失评估:**只看批次的损失或多或少有运气成分,计算模型在训练集和验证集上的平均损失
@torch.no_grad()
def estimate_loss():
out = {}
model.eval() # 评估模式: 关闭 dropout 层, 关闭 batchnorm 的统计更新
# 分别计算训练集和验证集损失
for split in ['train', 'val']:
losses = torch.zeros(eval_iters)
for k in range(eval_iters): # 随机 eval_iters 次取, 并计算平均损失
X, Y = get_batch(split)
logits, loss = model(X, Y)
losses[k] = loss.item()
out[split] = losses.mean()
model.train() # 恢复为训练模式
return out模型构建
最简单 bigram 模型,只基于当前 token 预测下一个 token,不考虑上下文信息,后续针对其进行优化
- B:批次大小 batch_size
- T:序列长度 block_size
- C:词汇表大小 vocab_size
class BigramLanguageModel(nn.Module):
def __init__(self):
super().__init__()
# 词嵌入层:每个token的索引都是字母表索引, 需要将其映射为向量, 可学习查找表, 训练过程中会更新
self.token_embedding_table = nn.Embedding(vocab_size, vocab_size)
self.lm_head = nn.Linear(n_embd, vocab_size)
def forward(self, idx, targets=None):
"""
idx: token 索引矩阵(B, T), targets: 目标 token 索引矩阵 (B, T)
"""
# 预测值
# logits = self.token_embedding_table(idx) # (B,T,C)
tok_emb = self.token_embedding_table(idx) # (B,T,C_emb)
logits = self.lm_head(tok_emb) # (B, T, C_vocab)
if targets is None:
loss = None
else:
B,T,C = logits.shape
# 适配 cross_entropy
logits = logits.view(B*T, C) # input: (样本数, 预测类别数)
targets = targets.view(B*T) # target: (每个样本真实类别索引, )
loss = F.cross_entropy(logits, targets)
return logits, loss
# 预测函数
def generate(self, idx, max_new_tokens): # (B, T) -> (B, T+max_new_tokens)
for _ in range(max_new_tokens):
logits, loss = self(idx)
logits = logits[:, -1, :] # 切片操作,取每个批次最后一个 token 的所有类别(B, C)
probs = F.softmax(logits, dim=-1) # 转换为概率分布: 每个batch中,对下一个token的概率分布 (B, C)
idx_next = torch.multinomial(probs, num_samples=1) # (B, 1) 个批次根据概率分布每对下一个采样预测
idx = torch.cat((idx, idx_next), dim=1) # (B, T+1) 拼接扩展序列
return idx
# m = BigramLanguageModel()
# logits, loss = m(xb, yb) # (4, 8, 65) # loss:4.8948 只是小批量的一个损失
# 预期损失为 -ln(1/65)=4.17 均值分布模型训练
模型实例
model = BigramLanguageModel()
m = model.to(device) # 使用 GPU优化器选择
optimizer = torch.optim.AdamW(m.parameters(), lr=learning_rate) # SGD: 随机梯度下降
# 典型良好学习率大约为 3e-4训练
for iter in range(max_iters):
if iter % eval_interval == 0:
losses = estimate_loss()
print(f"step {iter}: train loss {losses['train']:.4f}, val loss {losses['val']:.4f}")
xb, yb = get_batch('train')
logits, loss = model(xb, yb)
optimizer.zero_grad(set_to_none = True)
loss.backward()
optimizer.step()测试训练模型生成效果
context = torch.zeros((1, 1), dtype=torch.long, device=device)
print(decode(m.generate(context, max_new_tokens=500)[0].tolist())) # 类似格式但乱码数学核心机制
数学技巧学习:在自注意力机制中高效使用核心
B,T,C = 4, 8, 2 # batch, block, channels
x = torch.randn(B, T, C)需要这些 token 相互交流,弄清楚上下文有什么,使得更好预测接下来发生什么,且不可取未来的任何信息,想要与过去交流,最常见的方法是取过去至今的平均值,作为特征向量,概括上下文,但均值交流损失非常大,丢失了大量关于token的空间排列信息,实际平均值表示每个 token 之间的亲和力为 0
# 希望 x[b, t] = mean_{i<=t} x[b, i], bow:词袋
xbow = torch.zeros((B, T, C))
# 简单遍历
for b in range(B):
for t in range(T):
xprev = x[b, :t+1] # (t, C) 一个个加入, 表示先前有多少个 token
xbow[b, t] = torch.mean(xprev, 0) # 零维度求均值 (C)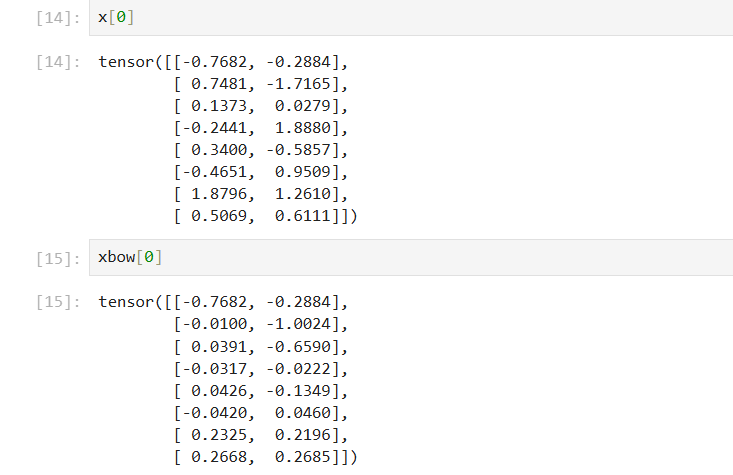
下三角矩阵特殊性(左下均为1)
a = torch.tril(torch.ones(3, 3))
a_mean = a / torch.sum(a, 1, keepdim=True)
b = torch.randint(0, 10, (3, 2)).float()
c = a @ b
d = a_mean @ b
"""
a:
tensor([[1., 0., 0.],
[1., 1., 0.],
[1., 1., 1.]])
a_mean:
tensor([[1.0000, 0.0000, 0.0000],
[0.5000, 0.5000, 0.0000],
[0.3333, 0.3333, 0.3333]])
b:
tensor([[1., 6.],
[8., 0.],
[7., 1.]])
c:
tensor([[ 1., 6.],
[ 9., 6.],
[16., 7.]])
d:
tensor([[1.0000, 6.0000],
[4.5000, 3.0000],
[5.3333, 2.3333]])
"""即可以使用矩阵乘法简化运算,通过下三角矩阵来代替实现求平均值,可并行运行加速
wei = torch.tril(torch.ones(T, T)) # 权重矩阵
wei = wei / wei.sum(1, keepdim=True) # (T, T)
#
xbow2 = wei @ x # (T, T) @ (B, T, C) 广播-> (B, T, T) @ (B, T, C) -> (B, T, C)
torch.allclose(xbow, xbow2) # true最终版本:使用下三角矩阵乘法来对过去的元素进行加权聚合
tril = torch.tril(torch.ones(T, T))
wei = torch.zeros((T, T))
wei = wei.masked_fill(tril == 0, float('-inf')) # 将 wei 中对应于 tril 中为 0 的位置设置为 -inf
"""
tensor([[0., -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., -inf],
[0., 0., 0., 0., 0., 0., 0., 0.]])
"""
wei = F.softmax(wei, dim=-1) # softmax: 取指数再均值
"""
tensor([[1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.5000, 0.5000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.3333, 0.3333, 0.3333, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.2500, 0.2500, 0.2500, 0.2500, 0.0000, 0.0000, 0.0000, 0.0000],
[0.2000, 0.2000, 0.2000, 0.2000, 0.2000, 0.0000, 0.0000, 0.0000],
[0.1667, 0.1667, 0.1667, 0.1667, 0.1667, 0.1667, 0.0000, 0.0000],
[0.1429, 0.1429, 0.1429, 0.1429, 0.1429, 0.1429, 0.1429, 0.0000],
[0.1250, 0.1250, 0.1250, 0.1250, 0.1250, 0.1250, 0.1250, 0.1250]])
"""
xbow3 = wei @ x
torch.allclose(xbow, xbow3) # true自注意力块编写
更新模型类
不仅要编码 token 身份,也要编码其位置,更新 __init__ 和 forward
class BigramLanguageModel(nn.Module):
def __init__(self):
super().__init__()
self.token_embedding_table = nn.Embedding(vocab_size, n_embd)
# 加入位置编码和语言模型头
self.position_embedding_table = nn.Embedding(block_size, n_embd)
self.lm_head = nn.Linear(n_embd, vocab_size)
def forward(self, idx, targets=None):
B, T = idx.shape
tok_emb = self.token_embedding_table(idx) # (B,T,C_emb)
pos_emb = self.position_embedding_table(torch.arange(T, device=device)) # (T, C_emb)
# 广播: (B,T,C_emb) + (T,C_emb) -> (B,T,C_emb) + (B,T,C_emb)
x = tok_emb + pos_emb
logits = self.lm_head(x) # (B, T, C_vocab)
if targets is None:
loss = None
else:
B,T,C = logits.shape
logits = logits.view(B*T, C)
targets = targets.view(B*T)
loss = F.cross_entropy(logits, targets)
return logits, loss自注意力核心
$$ Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}}) V $$
- 为单个头实现一个小型自注意力机制
- 最底层的除以根号下头大小:缩放注意力,保持方差不变
- 不希望一切都是均匀的,token 会发现其他不同的 token 更有趣或不那么有趣,需要有数据依赖,自注意力机制就是解决这个问题的
- 解决方案:每个位置的每个 token 会发出两个向量
- 查询向量:q(在寻找什么)
- 键向量:k(包含了什么)
- 亲和力:在键和查询间做点积,即自己本 token 的查询向量与所有其他 token 的键向量做点积
B, T, C = 4,8,32
x = torch.randn(B,T,C)
head_size = 16 # H
key = nn.Linear(C, head_size, bias=False) # 无偏置值
query = nn.Linear(C, head_size, bias=False)
value = nn.Linear(C, head_size, bias=False)
k = key(x) # (B,T,H)
q = query(x) # (B,T,H)
# 通信开始: 亲和力不再从0开始, 相当于每个 token 在知道自己包含的内容及处于的位置, 基于这些创建查询, 并与过去的 token 发出的键进行点积
wei = q @ k.transpose(-2, -1) # * head_size**-0.5 # (B,T,H) @ (B,H,T) = (B,T,T)
tril = torch.tril(torch.ones(T, T))
# wei = torch.zeros((T, T))
wei = wei.masked_fill(tril == 0, float('-inf')) # 禁止与未来通信
wei = F.softmax(wei, dim=-1) # 指数化及归一化
# out = wei @ x # (B, T, C)
v = value(x)
out = wei @ v # (B, T, H)
print(wei[0].round(decimals=2))把 x 看作是这个 token 的某种私有信息,v 是单头在不同节点间进行聚合后的内容,即先计算查询与每个内容索引的匹配度,softmax 分配权重找出最相关的内容,用这些权重加权求和内容
- 注意力 attention 是一种通信机制,有向图在自回归场景中具有的结构
- 若需要句子间完全相互通信,可删除掩码块,此时就对应自注意力编码器块
- 解码器块:未来无法影响过去和现在
- 自注意力:因为键、查询、值都来源于同一个源 x,而注意力可以不来源于一个源,所以还有交叉注意力
单头自注意力机制构建
class Head(nn.Module):
"""单头自注意力机制"""
def __init__(self, head_size):
super().__init__()
self.key = nn.Linear(n_embd, head_size, bias=False)
self.query = nn.Linear(n_embd, head_size, bias=False)
self.value = nn.Linear(n_embd, head_size, bias=False)
# 非参数则使用缓冲区
self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size)))
def forward(self, x):
B,T,C = x.shape
k = self.key(x)
q = self.query(x)
wei = q @ k.transpose(-2, -1) * C**-0.5
wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf'))
wei = F.softmax(wei, dim=-1)
v = self.value(x)
out = wei @ v
return out更新bigram模型类
- 减少学习率到 1e-3,由于注意力机制无法承受高的学习率,增加迭代次数
- 损失减小,但生成效果仍不佳
class BigramLanguageModel(nn.Module):
def __init__(self):
super().__init__()
self.token_embedding_table = nn.Embedding(vocab_size, n_embd)
self.position_embedding_table = nn.Embedding(block_size, n_embd)
# 加入
self.sa_head = Head(n_embd)
self.lm_head = nn.Linear(n_embd, vocab_size)
def forward(self, idx, targets=None):
B, T = idx.shape
tok_emb = self.token_embedding_table(idx)
pos_emb = self.position_embedding_table(torch.arange(T, device=device))
x = tok_emb + pos_emb
# 加入
x = self.sa_head(x)
logits = self.lm_head(x)
# 后续不变
# 预测函数
def generate(self, idx, max_new_tokens):
for _ in range(max_new_tokens):
# 确保输入序列不超过模型的上下文长度限制
idx_cond = idx[:, -block_size:]
logits, loss = self(idx_cond)
# 后续不变多头注意力机制
class MultiHeadAttention(nn.Module):
"""并行多头注意力机制"""
def __init__(self, num_heads, head_size):
super().__init__()
self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)]) # 创建多个独立 Head 模块
def forward(self, x):
# 每个注意力头独立处理相同输入 x, 并将所有头的输出在最后一个维度拼接
return torch.cat([h(x) for h in self.heads], dim = -1) # (B, T, num_heads * head_size)修改bigram模型,训练后损失下降到2.2-2.3左右,效果更好,出现类似的单词
# self.sa_head = Head(n_embd)
self.sa_heads = MultiHeadAttention(4, n_embd // 4) # 4 个并行
x = self.sa_heads(x)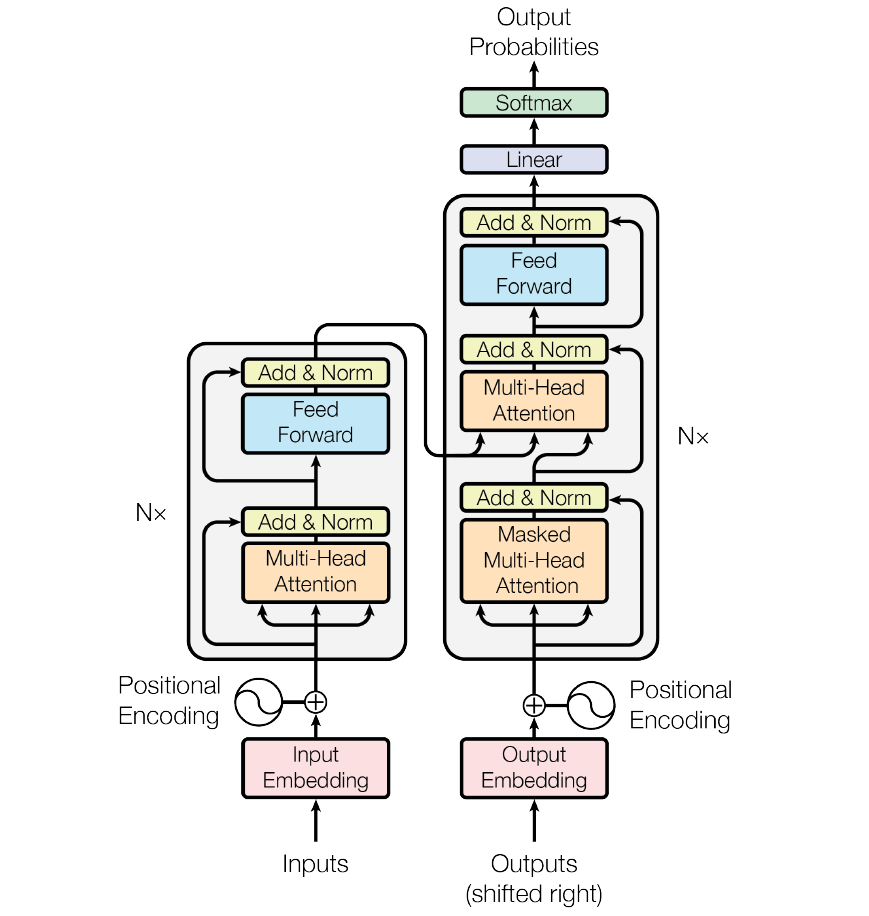
Feed Forward:位置感知前馈网络只是一个简单的小型多层感知机,类似于每个 token 在通信后独立思考这些数据
class FeedForward(nn.Module):
"""简单线性层+非线性层"""
def __init__(self, n_embd):
super().__init__()
self.net = nn.Sequential(
nn.Linear(n_embd, n_embd),
nn.ReLU(),
)
def forward(self, x):
return self.net(x)更新bigram模型,损失继续下降到2.2左右
# __init__ 在多头注意力机制后加入
self.ffwd = FeedForward(n_embd)
# forward 在 sa_heads 后加入
x = self.ffwd(x)Transformer 解码器构建
# 构建块
class Block(nn.Module):
"""Transformer block"""
def __init__(self, n_embd, n_head):
super().__init__()
head_size = n_embd // n_head
self.sa = MultiHeadAttention(n_head, head_size)
self.ffwd = FeedForward(n_embd)
def forward(self, x):
x = self.sa(x)
x = self.ffwd(x)
return x更新bigram模型,运行后效果不好,由于是深度神经网络,出现问题
# __init__
# self.sa_heads = MultiHeadAttention(4, n_embd // 4)
# self.ffwd = FeedForward(n_embd)
# 更换为
self.blocks = nn.Sequential(
Block(n_embd, n_head=4),
Block(n_embd, n_head=4),
Block(n_embd, n_head=4),
)
# forward
# x = self.sa_heads(x)
# x = self.ffwd(x)
# 更换为
x = self.blocks(x)优化方法
- 残差连接,或跳跃连接;通过加法将先前的特征中引入一个跳跃连接
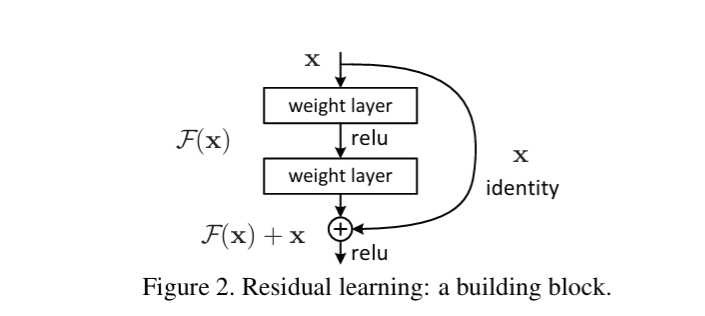
传播过程中,加法将梯度均匀分配给输入的两个分支,损失的梯度会跳过每一个加法节点,一直到达输入端,接着分叉进入残差块,损失降至2.11左右
# 多头注意力类更新
def __init__(self, num_heads, head_size):
super().__init__()
self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)])
self.proj = nn.Linear(n_embd, n_embd) # # 新增投影层
def forward(self, x):
# 拼接后 [batch_size, block_size, num_heads*head_size = n_embd]
# 多头注意力多个 head 拼接后特征空间分布变化
out = torch.cat([h(x) for h in self.heads], dim = -1)
# 投影层保证输入输出维度都是 n_embd
out = self.proj(out)
return out
# 前馈类更新
def __init__(self, n_embd):
super().__init__()
self.net = nn.Sequential(
nn.Linear(n_embd, 4 * n_embd),
nn.ReLU(),
nn.Linear(4 * n_embd, n_embd), # 投影层
)
# 构建块更新 forward, 残差连接本质: y = f(x) + x 所以 x 和 f(x) 维度必须一致
def forward(self, x):
x = x + self.sa(x)
x = x + self.ffwd(x)
return x- 层归一化
批归一化是对列(批次维度)归一化,而层归一化是对行(特征维度)归一化
- transformer 论文中 add&norm 是在变换之后应用的,但实际更常见的是变化之前应用归一化,所谓预归一化
class LayerNorm:
def __init__(self, dim, eps=1e-5):
self.eps = eps
self.gamma = torch.ones(dim)
self.beta = torch.zeros(dim)
def __call__(self, x):
xmean = x.mean(1, keepdim=True)
xvar = x.var(1, keepdim=True)
xhat = (x - xmean) / torch.sqrt(xvar + self.eps)
self.out = self.gamma * xhat + self.beta
return self.out实际更新构建块 Block 类,对每个样本的特征使其在初始化时具有单位均值和单位高斯分布
class Block(nn.Module):
"""Transformer block"""
def __init__(self, n_embd, n_head):
super().__init__()
head_size = n_embd // n_head
self.sa = MultiHeadAttention(n_head, head_size)
self.ffwd = FeedForward(n_embd)
self.ln1 = nn.LayerNorm(n_embd)
self.ln2 = nn.LayerNorm(n_embd)
def forward(self, x):
x = x + self.sa(self.ln1(x))
x = x + self.ffwd(self.ln2(x))
return x还需要更新 Bigram 模型
self.blocks = nn.Sequential(
Block(n_embd, n_head=4),
Block(n_embd, n_head=4),
Block(n_embd, n_head=4),
# 加入
nn.LayerNorm(n_embd),
)至此构建出了一个仅包含解码器的 transformer
进一步优化改动,A800 中运行,损失下降到 1.11 - 1.48
# 超参数更新
batch_size = 64
block_size = 256
max_iters = 5000
eval_interval = 500
learning_rate = 3e-4
eval_iters = 200
n_embd = 384
n_head = 6
n_layer = 6
dropout = 0.2
# Bigram 模型 __init__
# n_layer 指定有多少个 Block
self.blocks = nn.Sequential(*[Block(n_embd, n_head=n_head) for _ in range(n_layer)])
self.ln_f = nn.LayerNorm(n_embd)
# forward 加入
x = self.ln_f(x)
# FeedForward 层
self.net = nn.Sequential(
nn.Linear(n_embd, 4 * n_embd),
nn.ReLU(),
nn.Linear(4 * n_embd, n_embd),
# 加入 Dropout 层
nn.Dropout(dropout),
)
# 多头注意力机制类 __init__
self.dropout = nn.Dropout(dropout)
# forward 加入
out = self.dropout(self.proj(out))
# Head 类 __init__
self.dropout = nn.Dropout(dropout)
# forward softmax 后加入
wei = self.dropout(wei)最终代码
import torch
import torch.nn as nn
from torch.nn import functional as F
torch.manual_seed(1337)
batch_size = 64
block_size = 256
max_iters = 5000
eval_interval = 500
learning_rate = 3e-4
eval_iters = 200
n_embd = 384
n_head = 6
n_layer = 6
dropout = 0.2
device = 'cuda' if torch.cuda.is_available() else 'cpu'
with open('input.txt', 'r', encoding='utf-8') as f:
text = f.read()
chars = sorted(list(set(text)))
vocab_size = len(chars)
stoi = { ch:i for i,ch in enumerate(chars) }
itos = { i:ch for i,ch in enumerate(chars) }
encode = lambda s: [stoi[c] for c in s]
decode = lambda l: ''.join([itos[i] for i in l])
# 划分训练集和验证集
data = torch.tensor(encode(text), dtype=torch.long)
n = int(0.9*len(data))
train_data = data[:n]
val_data = data[n:]
def get_batch(split):
data = train_data if split == 'train' else val_data
ix = torch.randint(len(data) - block_size, (batch_size, ))
x = torch.stack([data[i:i+block_size] for i in ix])
y = torch.stack([data[i+1:i+block_size+1] for i in ix])
x, y = x.to(device), y.to(device)
return x, y
@torch.no_grad()
def estimate_loss():
out = {}
model.eval()
for split in ['train', 'val']:
losses = torch.zeros(eval_iters)
for k in range(eval_iters):
X, Y = get_batch(split)
logits, loss = model(X, Y)
losses[k] = loss.item()
out[split] = losses.mean()
model.train()
return out
class Head(nn.Module):
"""单头自注意力机制"""
def __init__(self, head_size):
super().__init__()
self.key = nn.Linear(n_embd, head_size, bias=False)
self.query = nn.Linear(n_embd, head_size, bias=False)
self.value = nn.Linear(n_embd, head_size, bias=False)
self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size)))
self.dropout = nn.Dropout(dropout)
def forward(self, x):
B,T,C = x.shape
k = self.key(x)
q = self.query(x)
wei = q @ k.transpose(-2, -1) * C**-0.5
wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf'))
wei = F.softmax(wei, dim=-1)
wei = self.dropout(wei)
v = self.value(x)
out = wei @ v
return out
class MultiHeadAttention(nn.Module):
"""并行多头注意力机制"""
def __init__(self, num_heads, head_size):
super().__init__()
self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)])
self.proj = nn.Linear(n_embd, n_embd)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
out = torch.cat([h(x) for h in self.heads], dim = -1)
out = self.dropout(self.proj(out))
return out
class FeedForward(nn.Module):
"""简单线性层+非线性层"""
def __init__(self, n_embd):
super().__init__()
self.net = nn.Sequential(
nn.Linear(n_embd, 4 * n_embd),
nn.ReLU(),
nn.Linear(4 * n_embd, n_embd),
nn.Dropout(dropout),
)
def forward(self, x):
return self.net(x)
class BigramLanguageModel(nn.Module):
def __init__(self):
super().__init__()
self.token_embedding_table = nn.Embedding(vocab_size, n_embd)
self.position_embedding_table = nn.Embedding(block_size, n_embd)
self.blocks = nn.Sequential(*[Block(n_embd, n_head=n_head) for _ in range(n_layer)])
self.ln_f = nn.LayerNorm(n_embd)
self.lm_head = nn.Linear(n_embd, vocab_size)
def forward(self, idx, targets=None):
B, T = idx.shape
tok_emb = self.token_embedding_table(idx) # (B,T,C_emb)
pos_emb = self.position_embedding_table(torch.arange(T, device=device))
x = tok_emb + pos_emb
x = self.blocks(x)
x = self.ln_f(x)
logits = self.lm_head(x) # (B, T, C_vocab)
if targets is None:
loss = None
else:
B,T,C = logits.shape
logits = logits.view(B*T, C)
targets = targets.view(B*T)
loss = F.cross_entropy(logits, targets)
return logits, loss
# 预测函数
def generate(self, idx, max_new_tokens): # (B, T) -> (B, T+max_new_tokens)
for _ in range(max_new_tokens):
idx_cond = idx[:, -block_size:]
logits, loss = self(idx_cond)
logits = logits[:, -1, :]
probs = F.softmax(logits, dim=-1)
idx_next = torch.multinomial(probs, num_samples=1)
idx = torch.cat((idx, idx_next), dim=1)
return idx
class Block(nn.Module):
"""Transformer block"""
def __init__(self, n_embd, n_head):
super().__init__()
head_size = n_embd // n_head
self.sa = MultiHeadAttention(n_head, head_size)
self.ffwd = FeedForward(n_embd)
self.ln1 = nn.LayerNorm(n_embd)
self.ln2 = nn.LayerNorm(n_embd)
def forward(self, x):
x = x + self.sa(self.ln1(x))
x = x + self.ffwd(self.ln2(x))
return x
model = BigramLanguageModel()
m = model.to(device) # 使用 GPU
optimizer = torch.optim.AdamW(m.parameters(), lr=learning_rate)
for iter in range(max_iters):
if iter % eval_interval == 0:
losses = estimate_loss()
print(f"step {iter}: train loss {losses['train']:.4f}, val loss {losses['val']:.4f}")
xb, yb = get_batch('train')
logits, loss = model(xb, yb)
optimizer.zero_grad(set_to_none = True)
loss.backward()
optimizer.step()
context = torch.zeros((1, 1), dtype=torch.long, device=device)
print(decode(m.generate(context, max_new_tokens=500)[0].tolist()))
"""
Had hypost proved the youthful lawful bead;
you was fall'n--one more, and two fair power them?
And non, more than the gage money--
How they have sinking itself, presently,
down yours that all approach your compalles!
Immercuited, in my tongue,
Give antime, and agreate sortents, I grieve point
The bodies, else that harres no which is elder.
GLOUCESTER:
Breath a truth, perish, what a king of secution
And that every my way sister of bride improdigred
And chembrate following great that which I nurs
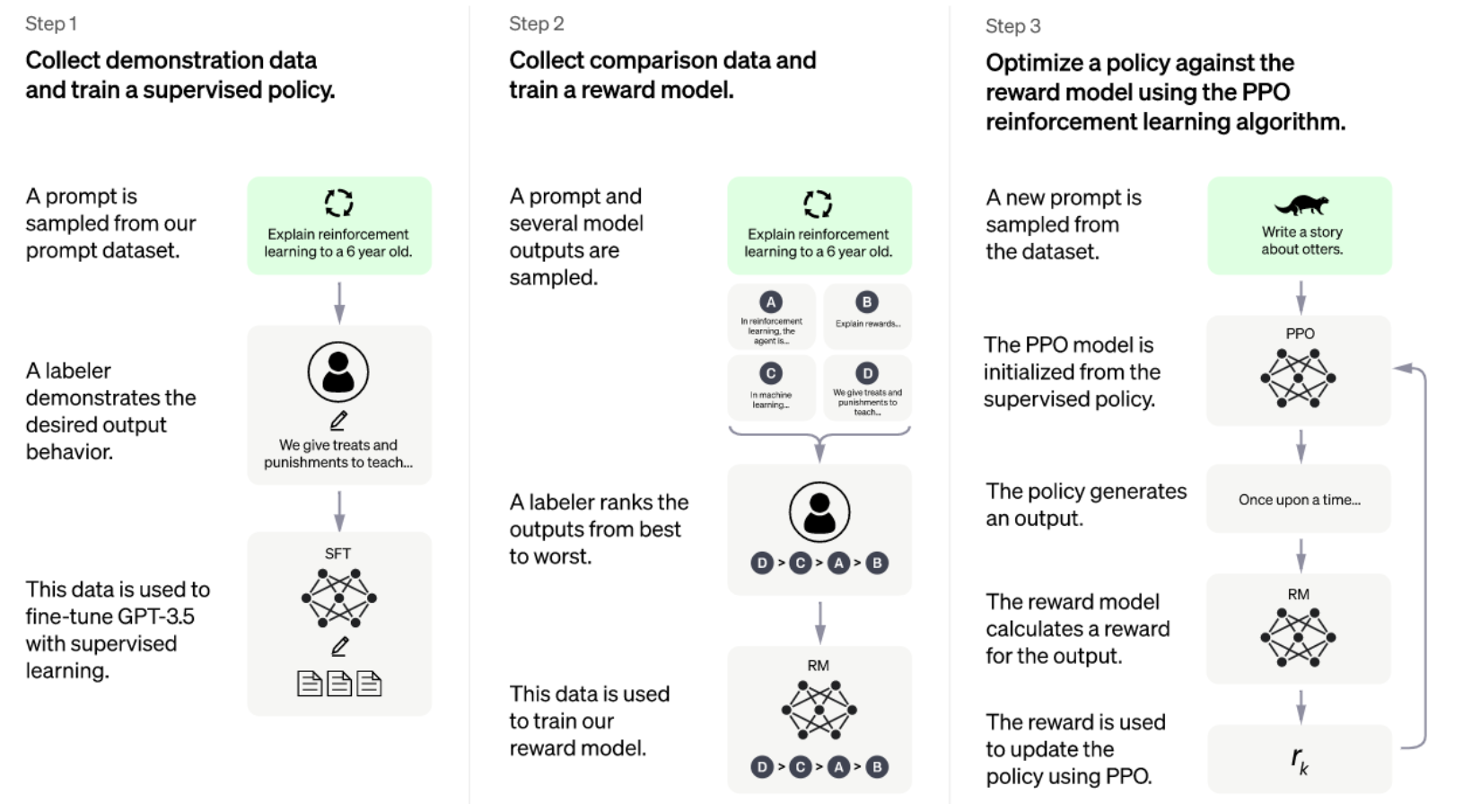
"""预训练阶段之后为微调阶段
Building GPT Tokenizer
在线测试:https://tiktokenizer.vercel.app/
- 嵌入向量为 50257 维,提高上下文长度到 1024 tokens
- 分词器影响:拼写正确性、非英语表现差、算术表现差
- 在非英语情况下,token 数量变大,导致上下文耗尽,效果差,使得文本膨胀
编码
test = "안녕하세요 👋 (hello in korean!)" # unicode 编码
print(ord("👋")) # 返回单个 unicode 字符的整数, 且定义了三种编码(utf-8, utf-16, utf-32)
print([ord(x) for x in test])
# utf-8 编码为字节流(1-4字节, 变长编码)
print(list(test.encode("utf-8"))) # 导致上下文长度过大实际希望不使用原始字节码,更希望能支持更大词汇量,并将其作为超参数进行调整,转向字节对编码算法(双极编码算法压缩)
# 不断迭代找出最频繁出现的双字节,将其编码为新的字符加入字典表
# 字典数 字符长
aaabdaaabac 4 11
ZabdZabac 5 9
Z=aa
ZYdZYac 6 7
Y=ab
Z=aa
XdXac 7 5
X=ZY
Y=ab
Z=aa 分词器编码解码器
算法第一步,迭代找出出现频率最高的字节对
text = "Unicode! 🅤🅝🅘🅒🅞🅓🅔‽ 🇺🇳🇮🇨🇴🇩🇪! 😄 The very name strikes fear and awe into the hearts of programmers worldwide. We all know we ought to “support Unicode” in our software (whatever that means—like using wchar_t for all the strings, right?). But Unicode can be abstruse, and diving into the thousand-page Unicode Standard plus its dozens of supplementary annexes, reports, and notes can be more than a little intimidating. I don’t blame programmers for still finding the whole thing mysterious, even 30 years after Unicode’s inception."
tokens = text.encode('utf-8')
tokens = list(map(int, tokens))
print("text_length: ", len(text), " len_tokens: ", len(tokens))
# 533 616
# 标记范围为 0 - 255
# 从不同的字节对映射到出现次数的字典
def get_stats(ids):
counts = {}
for pair in zip(ids, ids[1:]):
counts[pair] = counts.get(pair, 0) + 1
return counts
stats = get_stats(tokens)
print(sorted(((v, k) for k, v in stats.items()), reverse=True))
# 最多频率为 (101, 32) chr(101) = 'e', chr(32) = ' '
# 获取最大频率字节对
top_pair = max(stats, key=stats.get)
# print(top_pair)创建新标记:256
def merge(ids, pair, idx):
# 对于 ids 列表, 使用新标记 idx 替换所有连续出现的字节对 pair
newids = []
i = 0
while i < len(ids):
if i < len(ids) - 1 and ids[i] == pair[0] and ids[i+1] == pair[1]:
newids.append(idx)
i += 2
else:
newids.append(ids[i])
i += 1
return newids
tokens2 = merge(tokens, top_pair, 256)
print(tokens2)
print("length: ", len(tokens2)) # 596接着不断进行循环,基于超参数来决定迭代多少次,此处运行了 20 次
vocab_size = 276 # 需要的最终字典表大小
num_merges = vocab_size - 256
ids = list(tokens)
merges = {} # (int, int) -> int
for i in range(num_merges):
stats = get_stats(ids)
pair = max(stats, key=stats.get)
idx = 256 + i
print(f"merging {pair} into a new token {idx}")
ids = merge(ids, pair, idx)
merges[pair] = idx
# 添加的词汇元素越多,压缩比越大
print("tokens length: ", len(tokens)) # 616
print("ids length: ", len(ids)) # 451
print(f"compression ratio: {len(tokens) / len(ids):.2f}X") # 压缩比: 1.37X需要构建编码器和解码器,实现字符串和ID序列的转换
vocab = {idx: bytes([idx]) for idx in range(256)} # len: 256
for (p0, p1), idx in merges.items():
vocab[idx] = vocab[p0] + vocab[p1] # 拼接字节对象 len: 276- UTF-8 中单字节的有效范围是 0-127,若不使用 errors 会出现抛出异常
- 128-191(0x80-0xBF)是连续字节(continuation bytes),不能单独出现
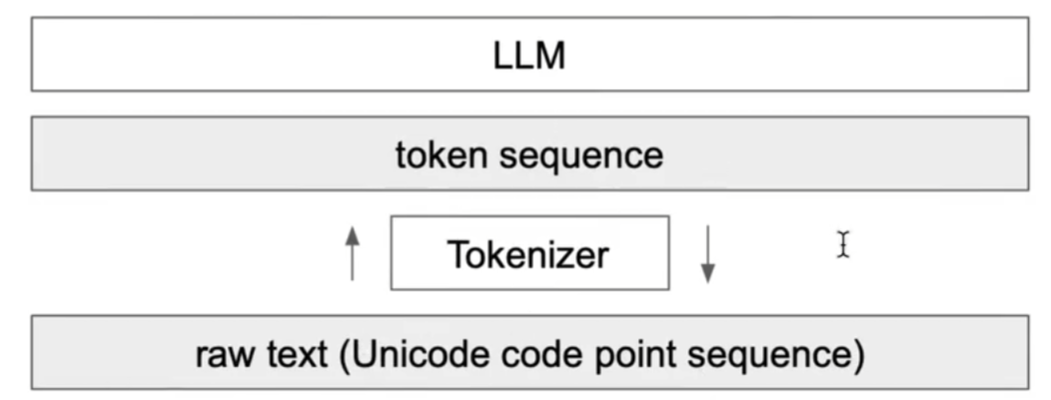
def decode(ids):
# 给定ID序列返回字符串
tokens = b"".join(vocab[idx] for idx in ids)
text = tokens.decode('utf-8', errors="replace")
return text
print(decode([128]))
# **BPE(Byte Pair Encoding)分词器**
def encode(text):
# 给定字符串返回ID序列
tokens = list(text.encode("utf-8"))
while len(tokens) >= 2:
stats = get_stats(tokens) # 统计相邻 token 对的出现频率
# 找到最应该合并的 pair, merges 中最小的值, 因为其从256不断往上加
pair = min(stats, key=lambda p: merges.get(p, float("inf")))
if pair not in merges:
break # 不再可合并
idx = merges[pair]
tokens = merge(tokens, pair, idx)
return tokens
print(encode("hello world"))实现了最简单的 tokenizer 配置
GPT 系列分词器
GPT2论文中:对于”dog!”, “dog?”这一类的词,BPE算法将其合并成单个 token,得到许多只是标点稍有不同的 “dog” 的 token,将不应该聚合的东西聚合在一起,不理想
- 使用人工自上而下保证,规定某些类型字符永远不应该合并在一起(通过正则实现)
import regex as re
gpt2pat = re.compile(r"""'s|'t|'re|'ve|'m|'ll|'d| ?\p{L}+| ?\p{N}+| ?[^\s\p{L}\p{N}]+|\s+(?!\S)|\s+""")
print(re.findall(gpt2pat, "hello'va 12world! How are you here "))
# ['hello', "'", 'va', ' 12', 'world', '!', ' How', ' are', ' you', ' ', ' here', ' ']
example = """
for i in range(1, 100):
if i % 3 == 0:
print("test")
else:
continue
"""
print(re.findall(gpt2pat, example))
# ['\n', 'for', ' i', ' in', ' range', '(', '1', ',', ' 100', '):', '\n ', ' if', ' i', ' %', ' 3', ' ==', ' 0', ':', '\n ', ' print', '("', 'test', '")', '\n ', ' else', ':', '\n ', ' continue', '\n']通过首先正则分成多个字符列表,再进行 tokenizer 转换为 ID 序列,再重新拼接,使得只会考虑单词之间的合并
Tiktoken 用于分词推理,词汇表大小从约 5 万增加到约 10 万
import tiktoken
# GPT-2
enc = tiktoken.get_encoding("gpt2")
print(enc.encode("test"))
# GPT-4
enc = tiktoken.get_encoding("cl100k_base")
print(enc.encode("test222"))理解 GPT-2 encoder.py 文件
- 加载的
encoder.json实际类似于vocab,而vocab.bpe即为merges
特殊 token
GPT-2 的 encoder 长度为 50257,即在 256 原始字节 token 中进行了 50000 次合并,还多一个 token 为:<|endoftext|> 特殊 token
sentencepiece
高效训练和推理 BPE 分词器,用于 Llama 和 Mistral 系列
- 直接用在 Unicode 编码上
import os
import sentencepiece as spm
with open("toy.txt", "w", encoding="utf-8") as f:
f.write("SentencePiece is an unsupervised text tokenizer and detokenizer mainly for Neural Network-based text generation systems where the vocabulary size is predetermined prior to the neural model training. SentencePiece implements subword units (e.g., byte-pair-encoding (BPE) [Sennrich et al.]) and unigram language model [Kudo.]) with the extension of direct training from raw sentences. SentencePiece allows us to make a purely end-to-end system that does not depend on language-specific pre/postprocessing.")
# 训练 sentencepiece 模型
# 训练 Llama2 的配置
options = dict(
input="toy.txt",
input_format="text",
model_prefix="tok400", # 输出文件名前缀
model_type="bpe",
vocab_size=400, # 词汇表大小
normalization_rule_name="identity",
remove_extra_whitespaces=False,
input_sentence_size=200000000, # 最大训练句子数
max_sentence_length=4192, # 每个句子最大字节数
seed_sentencepiece_size=1000000,
shuffle_input_sentence=True,
character_coverage=0.99995,
byte_fallback=True, # 字节回退 False 则不会使用字节编码
# 合并规则
split_digits=True,
split_by_unicode_script=True,
split_by_whitespace=True,
split_by_number=True,
max_sentencepiece_length=16,
add_dummy_prefix=True,
allow_whitespace_only_pieces=True,
unk_id=0, # 未知 token
bos_id=1, # 句子开始 token
eos_id=2, # 句子结束 token
pad_id=-1, # 填充 token
num_threads=os.cpu_count(),
)
# 训练后生成 tok400.model, tok400.vocab
spm.SentencePieceTrainer.Train(**options)加载模型实验
sp = spm.SentencePieceProcessor()
sp.load('tok400.model')
vocab = [[sp.id_to_piece(idx), idx] for idx in range(sp.get_piece_size())]
# print(vocab) # 400 词汇大小模型
# 特殊 token - 字节 token - merge token - 单独字符 token
ids = sp.encode("hello world")
print(ids)
print([sp.id_to_piece(idx) for idx in ids])
# [362, 378, 361, 372, 358, 313, 269, 372, 370]
# ['▁', 'h', 'e', 'l', 'lo', '▁w', 'or', 'l', 'd']Reproducing GPT-2
- https://github.com/openai/gpt-2,复现GPT-2时会同时参考GPT-3,nanoGPT
- 1.24亿参数,12 层,768个通道数
- https://huggingface.co/openai-community/gpt2
加载 GPT-2 模型
from transformers import GPT2LMHeadModel
import matplotlib.pyplot as plt
model_hf = GPT2LMHeadModel.from_pretrained("/data/models/gpt2") # 124M
sd_hf = model_hf.state_dict() # 模型状态字典 包含模型的所有可学习参数
for k, v in sd_hf.items():
print(k, v.shape)参数查看
# 词查找表 token embedding weight 字典表 50257, 768 维向量
transformer.wte.weight torch.Size([50257, 768])
# 位置查找表 position embedding weight 最大序列长度: 1024
transformer.wpe.weight torch.Size([1024, 768])
transformer.h.0.ln_1.weight torch.Size([768])
transformer.h.0.ln_1.bias torch.Size([768])
transformer.h.0.attn.c_attn.weight torch.Size([768, 2304])
transformer.h.0.attn.c_attn.bias torch.Size([2304])
transformer.h.0.attn.c_proj.weight torch.Size([768, 768])
transformer.h.0.attn.c_proj.bias torch.Size([768])
transformer.h.0.ln_2.weight torch.Size([768])
transformer.h.0.ln_2.bias torch.Size([768])
transformer.h.0.mlp.c_fc.weight torch.Size([768, 3072])
transformer.h.0.mlp.c_fc.bias torch.Size([3072])
transformer.h.0.mlp.c_proj.weight torch.Size([3072, 768])
transformer.h.0.mlp.c_proj.bias torch.Size([768])
transformer.h.1.ln_1.weight torch.Size([768])
transformer.h.1.ln_1.bias torch.Size([768])
transformer.h.1.attn.c_attn.weight torch.Size([768, 2304])
transformer.h.1.attn.c_attn.bias torch.Size([2304])
transformer.h.1.attn.c_proj.weight torch.Size([768, 768])
transformer.h.1.attn.c_proj.bias torch.Size([768])
transformer.h.1.ln_2.weight torch.Size([768])
transformer.h.1.ln_2.bias torch.Size([768])
transformer.h.1.mlp.c_fc.weight torch.Size([768, 3072])
transformer.h.1.mlp.c_fc.bias torch.Size([3072])
transformer.h.1.mlp.c_proj.weight torch.Size([3072, 768])
...
transformer.h.11.mlp.c_proj.bias torch.Size([768])
transformer.ln_f.weight torch.Size([768])
transformer.ln_f.bias torch.Size([768])
lm_head.weight torch.Size([50257, 768])可视化 GPT-2 模型位置编码向量
- 模型训练越多,将期望显示的图越平滑
plt.plot(sd_hf["transformer.wpe.weight"][:, 150])
plt.plot(sd_hf["transformer.wpe.weight"][:, 200])
plt.plot(sd_hf["transformer.wpe.weight"][:, 250])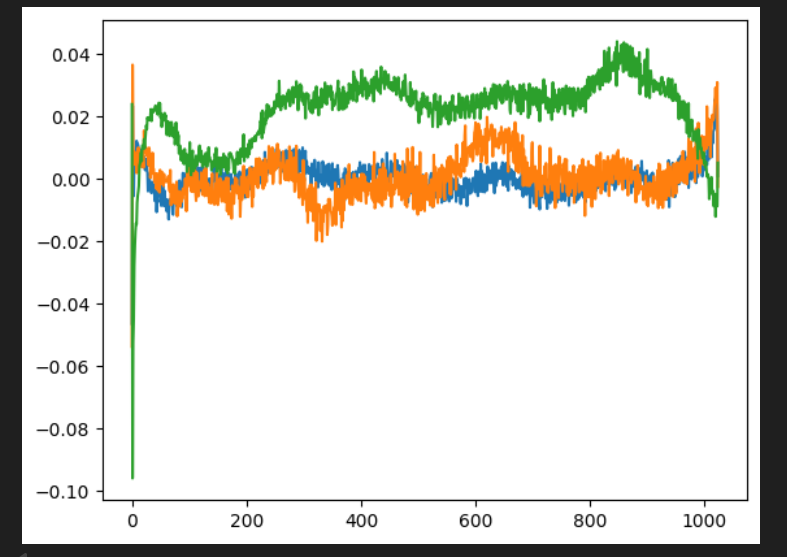
from transformers import pipeline, set_seed
generator = pipeline('text-generation', model='/data/models/gpt2')
set_seed(42)
generator("Hello, I'm a language model,", max_length=30, num_return_sequences=5)
# 使用生成内容构建模型类
导入
from dataclasses import dataclass
import torch
import torch.nn as nn
from torch.nn import functional as F
import math配置
@dataclass
class GPTConfig:
block_size: int = 256
vocab_size: int = 65
n_layer: int = 6
n_head: int = 6
n_embd: int = 384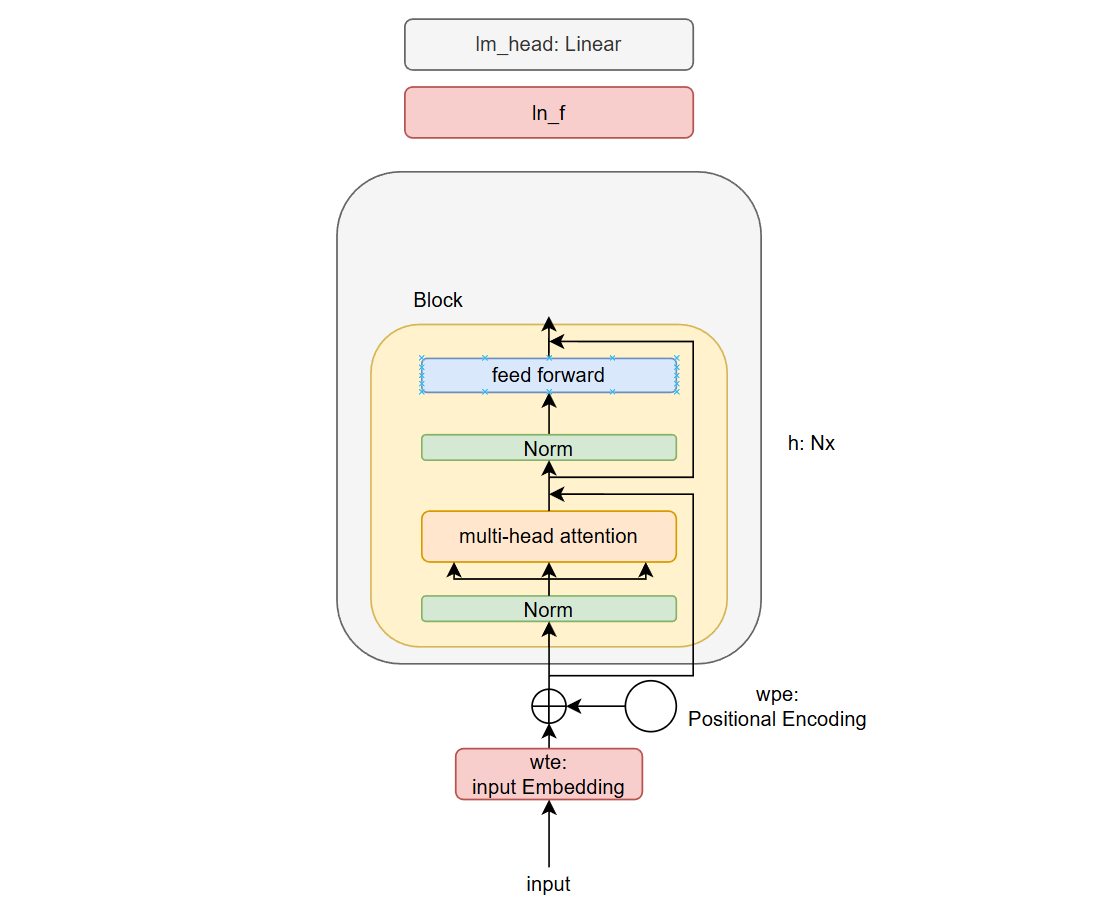
原始 transformer 中,层归一化在应用注意力或前馈后进行的,归一化在残差流内部进行即残差路径内包含了归一化, GPT-2 对 transformer 架构进行了轻微修改
- 无编码器,仅包含解码器,且也没有对应的交叉注意力部分
- 将层归一化提前,保证残差流清晰包含输入数据
其中,注意力是一种通信机制,所有 1024 个 token 按顺序排列,通信交换信息(聚合池化函数,权重和,归约操作); MLP 发生在每一个单独的 token 上(映射操作) ,即 transformer 类似于重复应用 MapReduce 的过程
基础模型构建
# 因果自注意力
class CausalSelfAttention(nn.Module):
def __init__(self, config):
super().__init__()
assert config.n_embd % config.n_head == 0
self.c_attn = nn.Linear(config.n_embd, 3 * config.n_embd)
self.c_proj = nn.Linear(config.n_embd, config.n_embd)
self.n_head = config.n_head
self.n_embd = config.n_embd
self.register_buffer("bias", torch.tril(torch.ones(config.block_size, config.block_size))
.view(1, 1, config.block_size, config.block_size))
def forward(self, x):
B, T, C = x.size() # B 个样本, 每个样本 T 个 token, 每个 token C 个嵌入向量编码
qkv = self.c_attn(x) # (B, T, 3*n_embd)
q, k, v = qkv.split(self.n_embd, dim=2) # 拆分: (B, T, n_embd)
# reshape: (B, n_head, T, C/n_head) 分成 n_head 个头并行处理
k = k.view(B, T, self.n_head, C // self.n_head).transpose(1, 2)
q = q.view(B, T, self.n_head, C // self.n_head).transpose(1, 2)
v = v.view(B, T, self.n_head, C // self.n_head).transpose(1, 2)
# 后两维度矩阵乘法->注意力分数计算: (B, n_head, T, T)
att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1)))
att = att.masked_fill(self.bias[:, :, :T, :T] == 0, float('-inf'))
att = F.softmax(att, dim=-1)
# 将注意力分数作为权重与 value 矩阵相乘 -> (B, n_head, T, C/n_head)
y = att @ v
# 转置后按序列合并所有的头-> (B, T, C)
y = y.transpose(1, 2).contiguous().view(B, T, C)
# 线性层: (B, T, C)
y = self.c_proj(y)
return y
class MLP(nn.Module):
def __init__(self, config):
super().__init__(self, config)
self.c_fc = nn.Linear(config.n_embd, 4 * config.n_embd)
self.gelu = nn.GELU(approximate='tanh')
self.c_proj = nn.Linear(4 * config.n_embd, config.n_embd)
def forward(self, x):
# -> (B, T, 4*n_embd)
x = self.c_fc(x)
# -> (B, T, 4*n_embd)
x = self.gelu(x)
# -> (B, T, n_embd)
x = self.c_proj(x)
return x
class Block(nn.Module):
def __init__(self, config):
super().__init__()
self.ln_1 = nn.LayerNorm(config.n_embd)
self.attn = CausalSelfAttention(config)
self.ln_2 = nn.LayerNorm(config.n_embd)
self.mlp = MLP(config)
def forward(self, x): # (B, T, n_embd)
# 层归一化: ln_1 -> (B, T, n_embd)
# 多头注意力机制: attn -> (B, T, n_embd)
# 残差: -> (B, T, n_embd)
x = x + self.attn(self.ln_1(x))
# 层归一化: ln_2 -> (B, T, n_embd)
# 多层感知机: mlp -> (B, T, n_embd)
# 残差: -> (B, T, n_embd)
x = x + self.mlp(self.ln_2(x))
return xGeLU:处处可导,完全非线性,缓解梯度消失
参数修改
@dataclass
class GPTConfig:
block_size: int = 1024
vocab_size: int = 50257
n_layer: int = 12
n_head: int = 12
n_embd: int = 768接管 huggingface 的所有权重,初始化 GPT
class GPT(nn.Module):
def __init__(self, config):
super().__init__()
self.config = config
self.transformer = nn.ModuleDict(dict(
wte = nn.Embedding(config.vocab_size, config.n_embd),
wpe = nn.Embedding(config.block_size, config.n_embd),
# 12 层隐藏层
h = nn.ModuleList([Block(config) for _ in range(config.n_layer)]),
# 最终线性归一层
ln_f = nn.LayerNorm(config.n_embd),
))
# 分类器: 语言模型头
self.lm_head = nn.Linear(config.n_embd, config.vocab_size, bias=False)
# 前向传播
def forward(self, idx):
# 同时处理 B 个样本, 每个样本 T 个 token
B, T = idx.size()
# 序列长度需要小于上下文大小
assert T <= self.config.block_size, f"Cannot forward sequence of length {T}, model block size is exhausted."
# 位置索引 (0 - T-1), shape: (T)
pos = torch.arange(0, T, dtype=torch.long, device=idx.device)
pos_emb = self.transformer.wpe(pos) # (T, n_embd)
tok_emb = self.transformer.wte(idx) # (B, T, n_embd)
x = tok_emb + pos_emb # 广播 (B, T, n_embd) 每个 token 有一串嵌入向量编码
for block in self.transformer.h:
x = block(x)
# block 后仍然为: (B, T, n_embd)
x = self.transformer.ln_f(x) # 层归一化
# 线性层, n_embd -> vocab_size
# (B, T, vocab_size) 在每个 B*T 的位置计算序列中下一个 token 的 logits
logits = self.lm_head(x)
return logits
@classmethod
def from_pretrained(cls, model_type):
"""从 huggingface 加载预训练 GPT-2 模型权重"""
assert model_type in {'gpt2', 'gpt2-medium', 'gpt2-large', 'gpt2-xl', '/data/models/gpt2'}
from transformers import GPT2LMHeadModel
print("loading weights from pretrained model: %s" % model_type)
config_args = {
'gpt2': dict(n_layer=12, n_head=12, n_embd=768), # 124M
'/data/models/gpt2': dict(n_layer=12, n_head=12, n_embd=768), # 124M
'gpt2-medium': dict(n_layer=24, n_head=16, n_embd=1024), # 350M
'gpt2-large': dict(n_layer=36, n_head=20, n_embd=1280), # 774M
'gpt2-xl': dict(n_layer=48, n_head=25, n_embd=1600), # 1558M
}[model_type]
config_args['vocab_size'] = 50257
config_args['block_size'] = 1024
config = GPTConfig(**config_args)
model = GPT(config)
sd = model.state_dict()
sd_keys = sd.keys()
sd_keys = [k for k in sd_keys if not k.endswith('.attn.bias')] # 排除缓冲区
model_hf = GPT2LMHeadModel.from_pretrained(model_type)
sd_hf = model_hf.state_dict()
sd_keys_hf = sd_hf.keys()
# 过滤掉 HuggingFace 模型中的缓冲区键
sd_keys_hf = [k for k in sd_keys_hf if not k.endswith('.attn.masked_bias')]
sd_keys_hf = [k for k in sd_keys_hf if not k.endswith('.attn.bias')]
# 定义需要转置的权重名称列表, 这些是线性层的权重, HuggingFace 和自定义实现中维度顺序不同
transposed = ['attn.c_attn.weight', 'attn.c_proj.weight', 'mlp.c_fc.weight', 'mlp.c_proj.weight']
assert len(sd_keys) == len(sd_keys_hf), f'dismatched keys: {len(sd_keys)} != {len(sd_keys_hf)}'
for k in sd_keys_hf:
if any(k.endswith(w) for w in transposed):
assert sd_hf[k].shape[::-1] == sd[k].shape # 转置后形状匹配
with torch.no_grad():
sd[k].copy_(sd_hf[k].t())
else:
assert sd_hf[k].shape == sd[k].shape
with torch.no_grad():
sd[k].copy_(sd_hf[k])
return model
model = GPT.from_pretrained('/data/models/gpt2')
print("Model loaded successfully.")构造输入前缀
num_return_sequences = 5
max_length = 30
model.eval()
model.to('cuda')
# 前缀 token
import tiktoken
enc = tiktoken.get_encoding("gpt2") # GPT-2 tokenizer
# 编码为 token 列表 [1, 2, ..., 8]
tokens = enc.encode("Hello, I'm a language model,")
# 转换为张量 ([1, ..., 8]) shape: (8)
tokens = torch.tensor(tokens, dtype=torch.long)
# unsqueeze(0) -> ([[1, ..., 8]]) shape: (1, 8)
# repeat -> shape: (5, 8) 输入 5 个样本, 每个样本 8 个 token 的上下文
tokens = tokens.unsqueeze(0).repeat(num_return_sequences, 1) # (5, 8)
x = tokens.to('cuda')生成序列
torch.manual_seed(42)
torch.cuda.manual_seed(42)
# 序列长度, x.size(1): 8, max_length: 30
while x.size(1) < max_length:
with torch.no_grad(): # 只进行生成
# 对每个样本的每个token都会生成一个未归一化的分数(logits)
logits = model(x) # (5, 8, 50257)
# 取每个样本的序列中最后一个 token 的 logits
logits = logits[:, -1, :] # (5, 50257)
# 转换为概率分布
probs = F.softmax(logits, dim=-1) # (5, 50257)
# top-k采样:只考虑概率最高的前k个token, (默认 50)
# topk_probs: 形状(5, 10),每个样本前10个最高概率 token 的概率
# topk_indices: 形状(5, 10),每个样本前10个最高概率 token 的词汇表索引
topk_probs, topk_indices = torch.topk(probs, k=10, dim=-1)
# 概率分布随机采样 1 个, 即尽管 top-10 的值是一样的,也会在 10 个中随机选一个, 不一定选概率最大的
ix = torch.multinomial(topk_probs, num_samples=1) # (5, 1)
# 获取实际的 token 词汇表索引
xcol = torch.gather(topk_indices, -1, ix) # (5, 1)
# 拼接
x = torch.cat((x, xcol), dim=1) # (5, 9)
for i in range(num_return_sequences):
tokens = x[i, :max_length].tolist()
decoded = enc.decode(tokens)
print(f"=== Sample {i+1} ===")
print(decoded) # 生成样例随机初始化训练
# 修改 model 不加载 huggingface 参数后, 运行生成随机返回
model = GPT(GPTConfig())GPU配置
device = 'cpu'
if torch.cuda.is_available():
device = 'cuda'
elif hasattr(torch.backends, 'mps') and torch.backends.mps.is_available():
device = 'mps'
print(f"using device: {device}")- 数据集使用:莎士比亚数据集
- 加载训练集和其对应的标签
device = 'cpu'
with open("input.txt", "r") as f:
text = f.read()
import tiktoken
enc = tiktoken.get_encoding("gpt2")
text = text[:1000]
tokens = enc.encode(text)
B, T = 4, 6
buf = torch.tensor(tokens[:B*T + 1])
buf = buf.to(device) # 张量存储在设备中需要返回新的张量
x = buf[:-1].view(B, T)
y = buf[1:].view(B, T)
print(x) # 输入
print(y) # 标签
model = GPT(GPTConfig())
model.to(device) # 就地存储在设备中
logits = model(x)
print(logits.shape)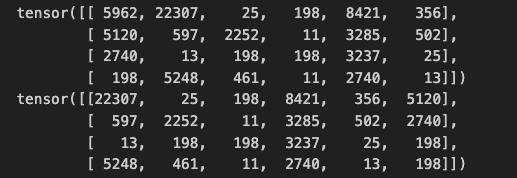
损失计算
# GPT forward 修改
def forward(self, idx, targets=None):
B, T = idx.size()
# 序列长度需要小于上下文大小
assert T <= self.config.block_size, f"Cannot forward sequence of length {T}, model block size is exhausted."
pos = torch.arange(0, T, dtype=torch.long, device=idx.device)
pos_emb = self.transformer.wpe(pos)
tok_emb = self.transformer.wte(idx)
x = tok_emb + pos_emb
for block in self.transformer.h:
x = block(x)
x = self.transformer.ln_f(x)
logits = self.lm_head(x)
loss = None
if targets is not None: # 三维转换为二维计算交叉熵损失
loss = F.cross_entropy(logits.view(-1, logits.size(-1)), targets.view(-1))
return logits, loss
logits, loss = model(x, y)
print(loss) # tensor(10.9893, grad_fn=<NllLossBackward0>)
# 初始理论损失为: -ln(1/50527) = 10.82490511**反向传播:**使用 GPU cuda
optimizer = torch.optim.AdamW(model.parameters(), lr=3e-4) # 用于早期对小批量进行测试
for i in range(50):
optimizer.zero_grad()
logits, loss = model(x, y)
loss.backward()
optimizer.step()
print(f"step {i+1}, loss: {loss.item():.4f}")数据加载器
之前是单个小批次进行训练,很容易导致过拟合,通过数据加载器运用在整个数据集中
class DataLoaderLite:
def __init__(self, B, T):
self.B = B
self.T = T
with open("input.txt", 'r') as f:
text = f.read()
enc = tiktoken.get_encoding("gpt2")
tokens = enc.encode(text)
self.tokens = torch.tensor(tokens)
print(f"loaded {len(self.tokens)} tokens") # 总 token 数量
# 一个 epoch 访问的 batch 数
print(f"1 epoch = {len(self.tokens) // (B * T)} batches")
# loaded 338024 tokens
# 1 epoch = 2640 batches
self.current_position = 0
def next_batch(self):
B, T = self.B, self.T
buf = self.tokens[self.current_position : self.current_position+B*T+1]
x = (buf[:-1]).view(B, T)
y = (buf[1:]).view(B, T)
self.current_position += B*T
if self.current_position + (B*T + 1) > len(self.tokens):
self.current_position = 0
return x, y
train_loader = DataLoaderLite(B=4, T=32)
model = GPT(GPTConfig())
model.to(device)
optimizer = torch.optim.AdamW(model.parameters(), lr=3e-4)
for i in range(50): # 只进行了 50/2640 批次的训练优化
x, y = train_loader.next_batch()
x, y = x.to(device), y.to(device)
optimizer.zero_grad()
logits, loss = model(x, y)
loss.backward()
optimizer.step()
print(f"step {i+1}, loss: {loss.item():.4f}")共享 WTE:输入嵌入层(Input Embedding)和输出投影层(Output Projection)共享同一个权重矩阵,可以减少参数量,节省时间
# 证明
print(sd_hf["lm_head.weight"].shape)
print(sd_hf["transformer.wte.weight"].shape)
print(sd_hf["lm_head.weight"] == sd_hf["transformer.wte.weight"]).all()
print(sd_hf["lm_head.weight"].data_ptr())
print(sd_hf["transformer.wte.weight"].data_ptr())
# GPT __init__ 中添加
# weight sharing scheme
self.transformer.wte.weight = self.lm_head.weight模型初始化:尝试使用公开的初始化
- OpenAI 公开的 GPT-2 代码中:
- 初始化时权重参数矩阵使用了 0.02 的标准差,偏差初始化为0,词元嵌入标准差初始化为 0.02,位置嵌入标准差初始化为 0.01
- 这些实际会随着模型增大而发生改变
# GPT 类中
# __init__ 末尾加入
# 初始化参数
self.apply(self._init_weights)
# 初始化权重参数函数
def _init_weights(self, module):
if isinstance(module, nn.Linear):
torch.nn.init.normal_(module.weight, mean=0.0, std=0.02)
if module.bias is not None:
torch.nn.init.zeros_(module.bias)
elif isinstance(module, nn.Embedding):
torch.nn.init.normal_(module.weight, mean=0.0, std=0.02)残差初始化
x = torch.zeros(768)
n = 100 # 100 层
for i in range(n):
x += torch.randn(768) # 模仿残差块
print(x.std()) # tensor(10.2873) 将会变得很大按照论文中处理:按照 根号N分之一 初始化,N 为残差层的数量
x += n**-0.5 * torch.randn(768)
# x.std(): tensor(1.0684) 控制前向传播中残差流内激活值增长的方法修改
# 对每个 c_proj 加入 (CausalSelfAttention, MLP)
self.c_proj.NANOGPT_SCALE_INIT = 1
# 修改 _init_weights
def _init_weights(self, module):
if isinstance(module, nn.Linear):
std = 0.02
if hasattr(module, 'NANOGPT_SCALE_INIT'):
std *= (2 * self.config.n_layer) ** -0.5
torch.nn.init.normal_(module.weight, mean=0.0, std=std)
if module.bias is not None:
torch.nn.init.zeros_(module.bias)
elif isinstance(module, nn.Embedding):
torch.nn.init.normal_(module.weight, mean=0.0, std=0.02)加速训练任务
nvidia-smi :查看显卡配置
import code; code.interact(local=locals()) # 可以用于断点调试训练第一次断点调试,logits.dtype 为 torch.float32 ,默认类型,32位浮点数表示,实际占用了相当多内存,经验表明,对于深度学习计算任务浪费,其可以容忍显著更低的精度
对于A100来说:TF32 可以提升 8 倍性能,BFloat 16 可以提升 16 倍性能,int 8 用于推理不用于训练,int 8 具有均匀间距,而需要适配神经网络的正态分布,不适合用 int 8
- 模型内存和带宽:有限 GPU 存储位数容量,以及访问内存的速度问题,特定内存带宽
- 张量核心是 A100 架构中的一个指令
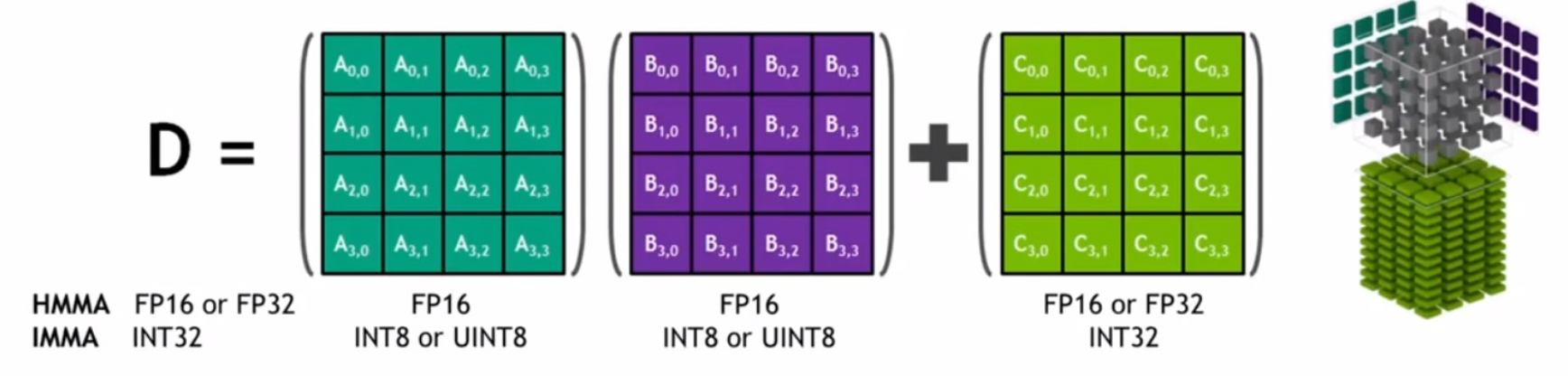
TF32 和 FP32 均有1个符号位,8个指数位,尾数位不同,截断13个,TF32 精度下降
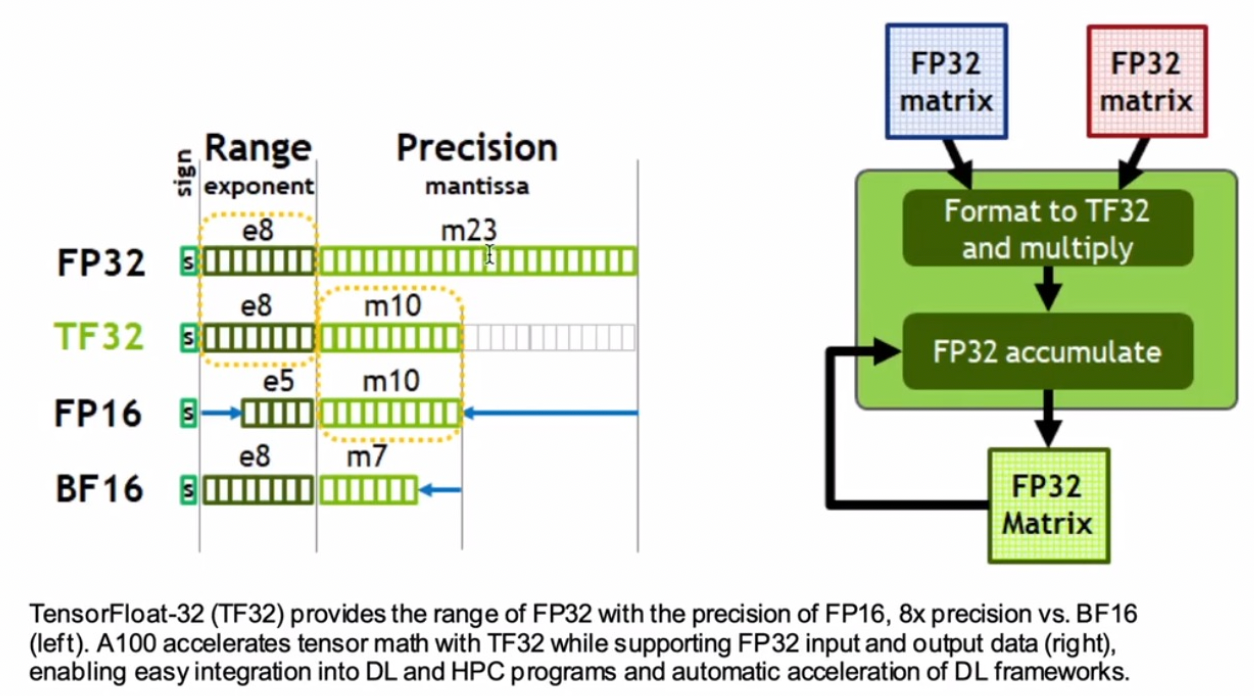
# 此时测试 B=16 T=1024
for i in range(50):
t0 = time.time()
x, y = train_loader.next_batch()
x, y = x.to(device), y.to(device)
optimizer.zero_grad()
logits, loss = model(x, y)
loss.backward()
optimizer.step()
torch.cuda.synchronize() # 等待 GPU 停止
t1 = time.time()
dt = (t1 - t0) * 1000
tokens_per_sec = (train_loader.B * train_loader.T) / (t1 - t0)
print(f"step {i+1}, loss: {loss.item():.4f}, time: {dt:.2f}ms, tok/sec: {tokens_per_sec:.2f}")
# 训练运行同时 watch -n 0.1 nvidia-smi
# 此时 FP32 每次 1100ms 左右, 35628MiB 内存占用, tok/sec: 15000 左右若超过GPU容量,尝试减少B的大小,尝试值:【8,16,24,32,48】等
测试 TF32:提升了 3 倍,受限于内存,仍然需要移动所有浮点数
# 加入
torch.set_float32_matmul_precision('high')
# 此时 TF32 每次 366ms 左右, 35628MiB 内存占用, tok/sec: 44500 左右测试 bfloat16:减少需要移动的浮点数,每个浮点数只保留16位
- 与 TF32 相比,指数位和符号位不变,精度位减少3位
- 模型参数此时仍是 fp32,但 logits 将变为 bf16
# 加入
x, y = x.to(device), y.to(device)
optimizer.zero_grad()
# 只有矩阵乘法会被转换为 bfloat16 计算, 其他仍为 FP32
with torch.autocast(device_type=device, dtype=torch.bfloat16):
logits, loss = model(x, y)
loss.backward()
# 此时 BFLOAT16 每次 305ms 左右, 33936MiB 内存占用, tok/sec: 53400 左右使用编译:加速
- GPU SRAM: 19TB/s(20MB)
- GPU HBM: 1.5TB/s(40GB)
- CPU DRAM: 12.8GB/s(>1TB)
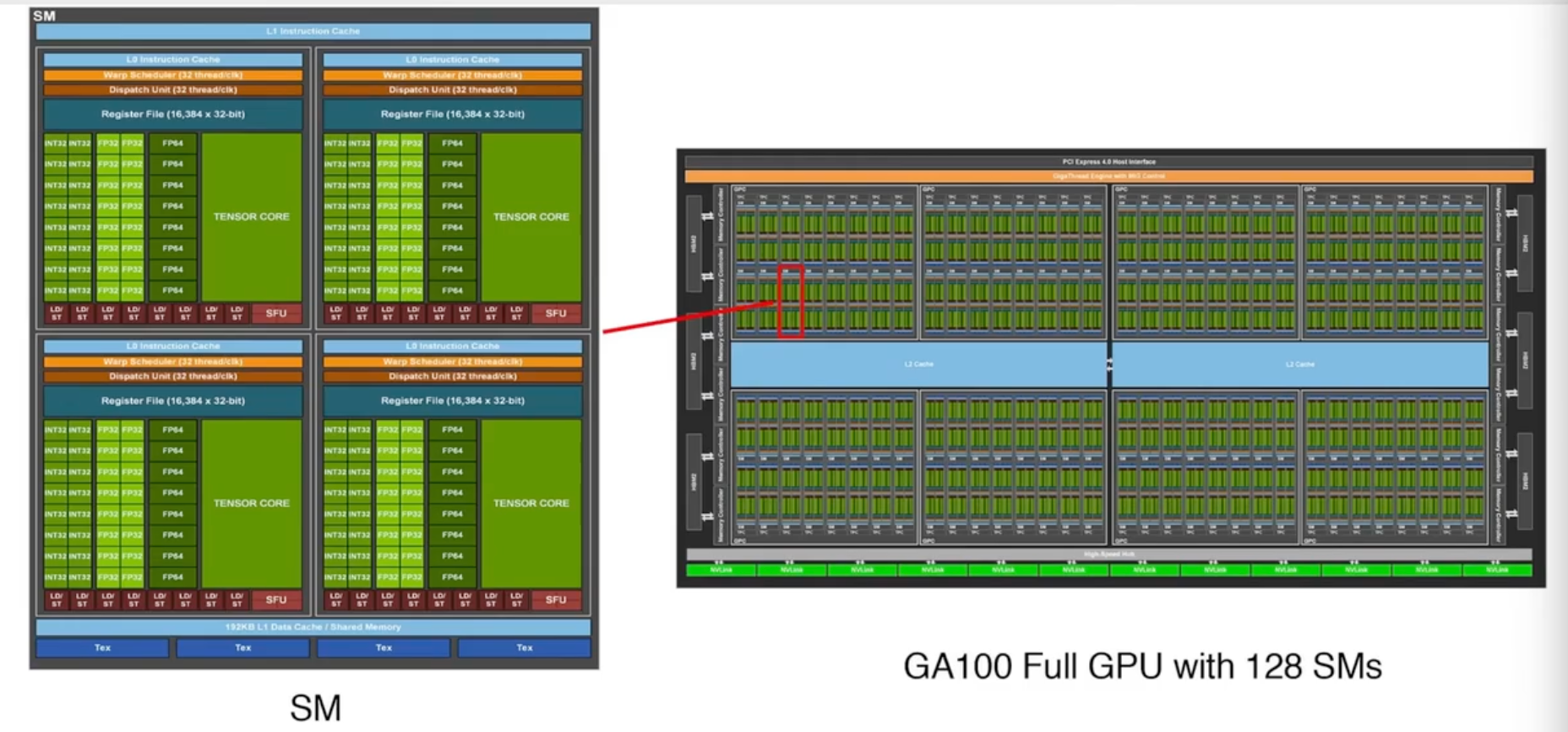
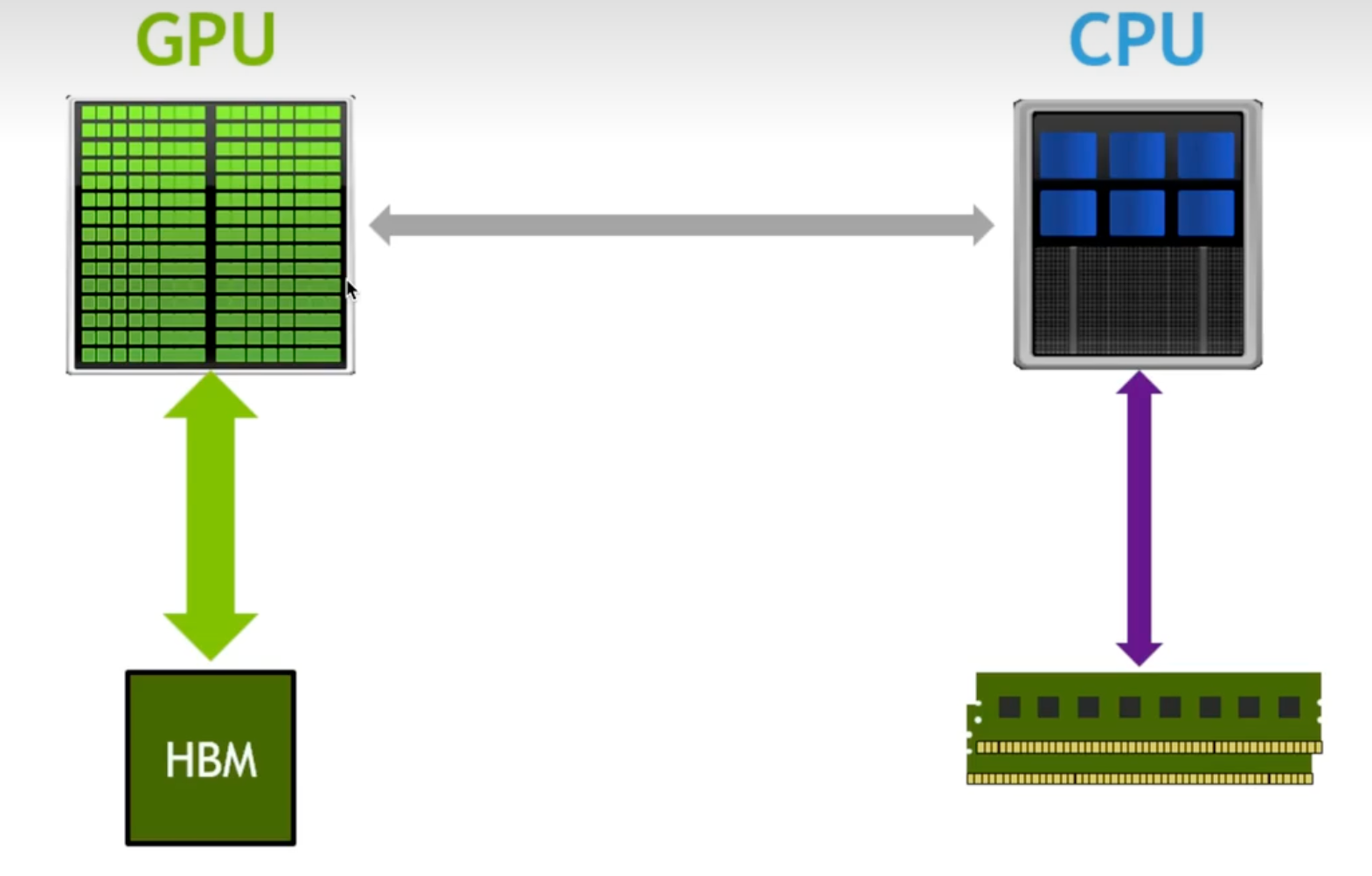
- 编译需要时间,加速主要来自于减少 python 开销和 GPU 读取次数,不再依靠python解释器
model = GPT(GPTConfig())
model.to(device)
model = torch.compile(model)
# 此时每次 136ms 左右, 23872MiB 内存占用, tok/sec: 118000 左右Flash Attention
- 2022,斯坦福,核融合技术,是 pytorch 编译无法发现的核融合,提高了 7 倍
- 注重内存层次结构,进行更多次浮点计算,但速度更快,基于对 softmax 的在线更新
# 替换以下代码
# att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1)))
# att = att.masked_fill(self.bias[:, :, :T, :T] == 0, float('-inf'))
# att = F.softmax(att, dim=-1)
# y = att @ v
y = F.scaled_dot_product_attention(q, k, v, is_causal=True)
# 此时每次 99ms 左右, 14578MiB 内存占用, tok/sec: 163500 左右数值改变优化:尝试使用2的幂次数,而减少其他数值
# 覆盖数值
# vocab_size 原先为 50257
model = GPT(GPTConfig(vocab_size=50304))
# 此时每次 97ms 左右, 13022MiB 内存占用, tok/sec: 168000 左右转向 GPT-3 设置参数
- 变化非常少,架构基本一致,上下文长度从 1024 扩展到 2048,GPT-3在更大数据集上训练了更长时间,有更全面的评估,GPT-3参数量为175B
- Adam 确保 beta1=0.9, beta2=0.95 参数和 epsilon=10^-8 参数
optimizer = torch.optim.AdamW(model.parameters(), lr=3e-4, betas=(0.9, 0.95), eps=1e-8) - 将梯度的全局范数裁剪到1.0,裁剪到某个最大范数,在计算梯度后立即插入一行代码
- 梯度裁剪,防止梯度爆炸,将所有参数的梯度限制在一个最大值内
- 若某批次可能会得到非常高的损失,高损失可能导致非常高的梯度,冲击模型和优化过程
loss.backward()
norm = torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0) # 计算参数的全局范数
# 参数向量的范数:对所有参数的每一个梯度,平方相加,取和的平方根
print(f"step {i+1}, loss: {loss.item():.4f}, norm: {norm:.4f}, time: {dt:.2f}ms, tok/sec: {tokens_per_sec:.2f}")余弦衰减学习率调度
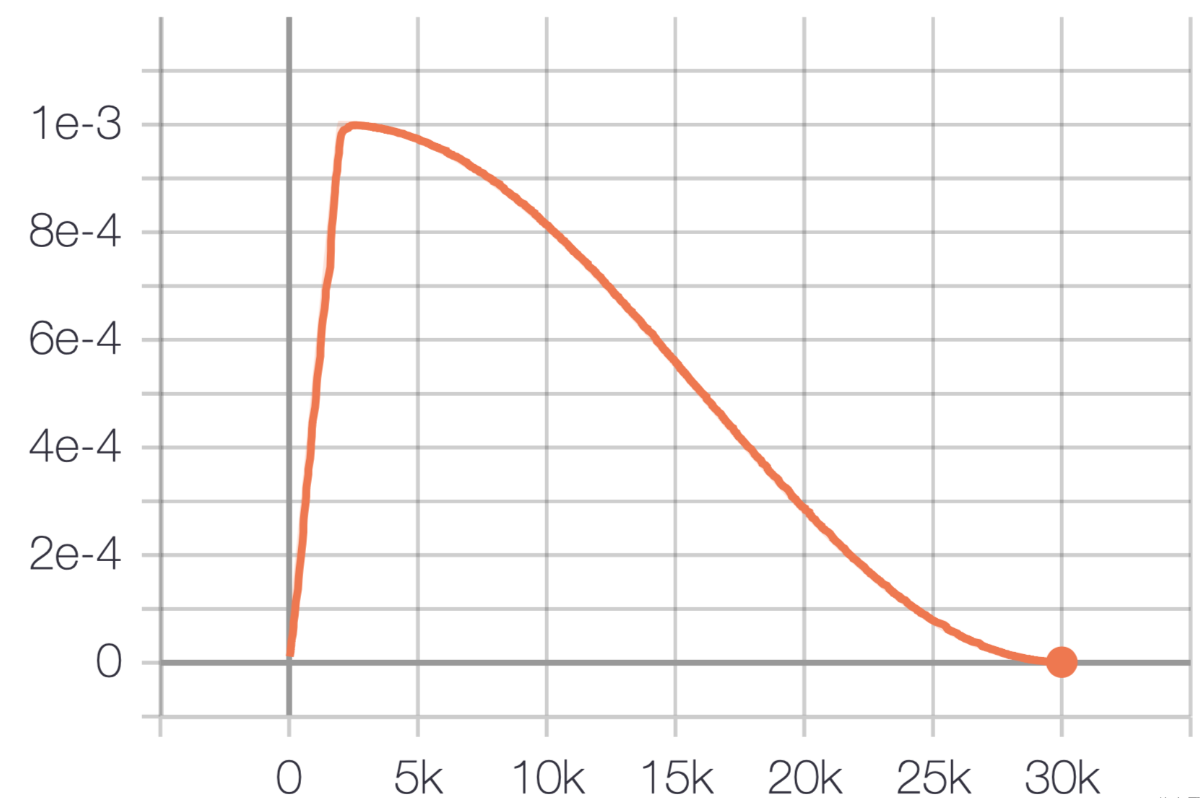
- 预热阶段,在某个范围内进行余弦衰减到 10%
max_lr = 6e-4
min_lr = max_lr * 0.1
warmup_steps = 10
max_steps = 50
def get_lr(it):
# 线性预热
if it < warmup_steps:
return max_lr * (it+1) / warmup_steps
# 超过最大步数, 返回最小学习率
if it > max_steps:
return min_lr
# 余弦衰减学习率到最小学习率
decay_ratio = (it - warmup_steps) / (max_steps - warmup_steps)
assert 0 <= decay_ratio <= 1
coeff = 0.5 * (1.0 + math.cos(math.pi * decay_ratio)) # 1 -> 0
return min_lr + coeff * (max_lr - min_lr)
for step in range(max_steps):
t0 = time.time()
x, y = train_loader.next_batch()
x, y = x.to(device), y.to(device)
optimizer.zero_grad()
with torch.autocast(device_type=device, dtype=torch.bfloat16):
logits, loss = model(x, y)
loss.backward()
norm = torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
lr = get_lr(step)
for param_group in optimizer.param_groups:
param_group['lr'] = lr
optimizer.step()
torch.cuda.synchronize() # 等待 GPU 停止
t1 = time.time()
dt = (t1 - t0) * 1000
tokens_processed = train_loader.B * train_loader.T
tokens_per_sec = tokens_processed / (t1 - t0)
print(f"step {step:4d}, loss: {loss.item():.4f}, lr: {lr:.4e}, norm: {norm:.4f}, time: {dt:.2f}ms, tok/sec: {tokens_per_sec:.2f}")在训练中无放回的抽取样本的数据处理方式,模型使用0.1的权重衰减来提供少量正则化
权重衰减实现
- 权重衰减意义:可以看做一种正则化,将所有权重都拉下来时,迫使优化使用更多的权重,不允许任何一个权重单独变得过大,迫使网络在更多通道上分配工作
import inspect
# GPT 类 weight_decay: 权重衰减系数(L2正则化)
def configure_optimizers(self, weight_decay, learning_rate, device):
# 获取所有参数(名称, 参数张量)
param_dict = {pn: p for pn, p in self.named_parameters()}
# 只保留梯度更新的参数
param_dict = {pn: p for pn, p in param_dict.items() if p.requires_grad}
# 按维度区分是否权重衰减(维度高防止过拟合,维度低防止欠拟合)
decay_params = [p for n, p in param_dict.items() if p.dim() >= 2] # 对嵌入向量和参与矩阵乘法的权重进行衰减
nodecay_params = [p for n, p in param_dict.items() if p.dim() < 2] # 一维张量
# 优化器组
optim_groups = [
{'params': decay_params, 'weight_decay': weight_decay},
{'params': nodecay_params, 'weight_decay': 0.0}
]
# 统计参数数量
num_decay_params = sum(p.numel() for p in decay_params)
num_nodecay_params = sum(p.numel() for p in nodecay_params)
print(f"num decayed parameter tensors: {len(decay_params)}, with {num_decay_params:,} parameters")
print(f"num non-decayed parameter tensors: {len(nodecay_params)}, with {num_nodecay_params:,} parameters")
# 检查fused AdamW是否可用
fused_available = 'fused' in inspect.signature(torch.optim.AdamW).parameters
use_fused = fused_available and 'cuda' in device
print(f"using fused AdamW: {use_fused}")
# 创建AdamW优化器
optimizer = torch.optim.AdamW(optim_groups, lr=learning_rate, betas=(0.9, 0.95), eps=1e-8, fused=use_fused)
return optimizer
# 修改优化器
optimizer = model.configure_optimizers(weight_decay=0.1, learning_rate=6e-4, device=device)
# 运行
# num decayed parameter tensors: 50, with 124,354,560 parameters
# num non-decayed parameter tensors: 98, with 121,344 parameters
# 此时每次 93ms 左右, tok/sec: 176000 左右, 且可见 loss, lr, norm较大的网络用较低的学习率进行训练,小网络使用小批量大小,大网络使用大批量大小,代码中 B 是样本数量,不是批量大小(batch_size),GPT-3 论文中的 batch_size 为 0.5M,即 B = 0.5M/T = 0.5M/1024 = 488,若 B 设置为 488,显存不够
梯度累积
- 有限 GPU 下模拟大批次训练,通过 B*T 进入 transformer 但不进行参数更新,而是在多次前向反向传播后再更新参数
total_batch_size = 524288 # 期望的总批次大小
B = 16 # 微批次大小
T = 1024
assert total_batch_size % (B * T) == 0, "make sure total_batch_size is divisible by B*T"
grad_accum_steps = total_batch_size // (B * T) # 32次 进行 32 次前向传播、反向传播然后进行一次梯度更新
print(f"total desired batch size: {total_batch_size}")
print(f"=> calculated gradient accumulations steps: {grad_accum_steps}")
train_loader = DataLoaderLite(B=B, T=T)修改训练代码(但该代码实际有错误),
for step in range(max_steps):
t0 = time.time()
optimizer.zero_grad()
for micro_step in range(grad_accum_steps): # 进行 grad_accum_steps 次循环
x, y = train_loader.next_batch()
x, y = x.to(device), y.to(device)
with torch.autocast(device_type=device, dtype=torch.bfloat16):
logits, loss = model(x, y)
loss.backward() # 梯度以加法方式累加到梯度张量上
norm = torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)错误问题思考
import torch
net = torch.nn.Sequential(
torch.nn.Linear(16, 32),
torch.nn.GELU(),
torch.nn.Linear(32, 1)
)
torch.random.manual_seed(42)
x = torch.randn(4, 16)
y = torch.randn(4, 1)
net.zero_grad()
yhat = net(x)
loss = torch.nn.functional.mse_loss(yhat, y)
loss.backward()
print(net[0].weight.grad.view(-1)[:10]) # 梯度
# 均方误差损失目标: 4 个样本
# L = 1/4 * [
# (y[0] - yhat[0])**2 +
# (y[1] - yhat[1])**2 +
# (y[2] - yhat[2])**2 +
# (y[3] - yhat[3])**2
# ]
# 梯度结果:
# tensor([-0.0150, 0.0011, 0.0042, -0.0040, 0.0059, -0.0080, -0.0078, -0.0138, -0.0103, -0.0134])梯度累积
# 涉及到梯度累积版本, 加入归一化后相当于在每个L前乘以1/4
# L0 = (y[0] - yhat[0])**2
# L1 = (y[1] - yhat[1])**2
# L2 = (y[2] - yhat[2])**2
# L3 = (y[3] - yhat[3])**2
# L = L0 + L1 + L2 + L3
# 1/4 被忽略
net.zero_grad()
for i in range(4):
yhat = net(x[i])
loss = torch.nn.functional.mse_loss(yhat, y[i])
# 加入归一化
loss = loss / 4
loss.backward()
print(net[0].weight.grad.view(-1)[:10])
# 梯度结果
# tensor([-0.0598, 0.0042, 0.0167, -0.0161, 0.0235, -0.0320, -0.0311, -0.0550, -0.0410, -0.0536])
# 优化后
# tensor([-0.0150, 0.0011, 0.0042, -0.0040, 0.0059, -0.0080, -0.0078, -0.0138, -0.0103, -0.0134])梯度不相同的原因是均方误差损失中的 1/4 被忽略了,完善训练代码
for step in range(max_steps):
t0 = time.time()
optimizer.zero_grad()
loss_accum = 0.0 # 创建损失累加器
for micro_step in range(grad_accum_steps): # 进行 grad_accum_steps 次循环
x, y = train_loader.next_batch()
x, y = x.to(device), y.to(device)
with torch.autocast(device_type=device, dtype=torch.bfloat16):
logits, loss = model(x, y)
loss = loss / grad_accum_steps
loss_accum += loss.detach() # 打印微批次的最终损失
loss.backward() # 梯度以加法方式累加到梯度张量上
norm = torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
lr = get_lr(step)
for param_group in optimizer.param_groups:
param_group['lr'] = lr
optimizer.step()
torch.cuda.synchronize() # 等待 GPU 停止
t1 = time.time()
dt = (t1 - t0) * 1000
tokens_processed = train_loader.B * train_loader.T * grad_accum_steps
tokens_per_sec = tokens_processed / (t1 - t0)
print(f"step {step:4d}, loss: {loss_accum.item():.4f}, lr: {lr:.4e}, norm: {norm:.4f}, time: {dt:.2f}ms, tok/sec: {tokens_per_sec:.2f}")继续训练,输出,损失乘以了 32 倍
using device: cuda
total desired batch size: 524288
=> calculated gradient accumulations steps: 32
loaded 338024 tokens
1 epoch = 20 batches
num decayed parameter tensors: 50, with 124,354,560 parameters
num non-decayed parameter tensors: 98, with 121,344 parameters
using fused AdamW: True分布式数据并行
- pytorch 的 DistributedDataParallel,启动多个进程,每个进程分配一个GPU
- 进行初始配置,修改设备情况
from torch.distributed import init_process_group, destroy_process_group
import torch.distributed as dist
# 设置 DDP (distributed data parallel 分布式数据并行)
ddp = int(os.environ.get('RANK', -1)) != -1 # 存在则为 DDP, 不存在或为-1则为单卡运行
if ddp:
# 检查 CUDA 可用性
assert torch.cuda.is_available(), "for now i think we need CUDA for DDP"
init_process_group(backend='nccl') # 初始化进程组 nccl: NVIDIA Collective Communications Library
# 获取分布式环境变量
ddp_rank = int(os.environ['RANK']) # 全局进程ID
ddp_local_rank = int(os.environ['LOCAL_RANK']) # 节点内进程ID
ddp_world_size = int(os.environ['WORLD_SIZE']) # 总进程数
# 设备设置
device = f'cuda:{ddp_local_rank}'
torch.cuda.set_device(device)
# 主进程(日志记录、保存检查点)
master_process = ddp_rank == 0
else:
ddp_rank = 0
ddp_local_rank = 0
ddp_world_size = 1 # 1 个进程
master_process = True # 单进程: 主进程
# 自动检测可用设备
device = "cpu"
if torch.cuda.is_available():
device = "cuda"
elif hasattr(torch.backends, "mps") and torch.backends.mps.is_available():
device = "mps"
print(f"using device: {device}")
# 修改
grad_accum_steps = total_batch_size // (B * T * ddp_world_size)
if master_process:
print(f"total desired batch size: {total_batch_size}")
print(f"=> calculated gradient accumulations steps: {grad_accum_steps}")修改数据加载器
- 每个进程需要处理不同的数据
- 所有进程的数据合起来覆盖整个数据集
class DataLoaderLite:
def __init__(self, B, T, process_rank, num_processes):
self.B = B
self.T = T
self.process_rank = process_rank # 当前进程 rank
self.num_processes = num_processes # 总进程数
with open("input.txt", 'r') as f:
text = f.read()
enc = tiktoken.get_encoding("gpt2")
tokens = enc.encode(text)
self.tokens = torch.tensor(tokens)
print(f"loaded {len(self.tokens)} tokens")
self.current_position = self.B * self.T * self.process_rank
def next_batch(self):
B, T = self.B, self.T
buf = self.tokens[self.current_position : self.current_position+B*T+1]
x = (buf[:-1]).view(B, T)
y = (buf[1:]).view(B, T)
self.current_position += B*T*self.num_processes
if self.current_position + (B*T*self.num_processes + 1) > len(self.tokens):
self.current_position = self.B * self.T * self.process_rank
return x, y
train_loader = DataLoaderLite(B=B, T=T, process_rank=ddp_rank, num_processes=ddp_world_size)封装模型
from torch.nn.parallel import DistributedDataParallel as DDP
# compile 后
if ddp:
model = DDP(model, device_ids=[ddp_local_rank])
raw_model = model.module if ddp else modelDDP默认每次backward()后自动同步梯度,但梯度累积需要累积多次后才同步一次
loss_accum += loss.detach()
if ddp:
model.require_backward_grad_sync = (micro_step == grad_accum_steps - 1)
loss.backward()优化器修改
optimizer = raw_model.configure_optimizers(weight_decay=0.1, learning_rate=6e-4, device=device)平均损失误差
# 在每次 micro_step 循环一遍后
if ddp:
dist.all_reduce(loss_accum, op=dist.ReduceOp.AVG)
...
tokens_processed = train_loader.B * train_loader.T * grad_accum_steps * ddp_world_size
tokens_per_sec = tokens_processed / (t1 - t0)
if master_process:
print(f"step {step:4d}, loss: {loss_accum.item():.4f}, lr: {lr:.4e}, norm: {norm:.4f}, time: {dt:.2f}ms, tok/sec: {tokens_per_sec:.2f}")销毁进程
if ddp:
destroy_process_group()运行:torchrun --standalone --nproc_per_node=2 gpt2.py
数据集
- redpajama/slimpajama, fineweb, fineweb-edu,数据混合
- 选择 fineweb-edu 的 10BT 数据进行实验
# 下载数据集
import os
import multiprocessing as mp
import numpy as np
import tiktoken
from datasets import load_dataset
from tqdm import tqdm
os.environ["HTTP_PROXY"] = "http://127.0.0.1:7890"
os.environ["HTTPS_PROXY"] = "http://127.0.0.1:7890"
local_dir = "edu_fineweb10B"
remote_name = "sample-10BT"
shard_size = int(1e8) # 100 个分片, 每个分片1亿token
DATA_CACHE_DIR = os.path.join(os.path.dirname(__file__), local_dir)
os.makedirs(DATA_CACHE_DIR, exist_ok=True)
fw = load_dataset("HuggingFaceFW/fineweb-edu", name=remote_name, split="train")
# 分词器 tokenizer 初始化
enc = tiktoken.get_encoding("gpt2")
eot = enc._special_tokens['<|endoftext|>'] # end of text token
def tokenize(doc):
"""单文档分词, 返回 uint16 类型 numpy 数组"""
tokens = [eot] # the special <|endoftext|> token delimits all documents
tokens.extend(enc.encode_ordinary(doc["text"])) # 对 text 内容分词
tokens_np = np.array(tokens)
# 所有 token 在 0-65535 范围内
assert (0 <= tokens_np).all() and (tokens_np < 2**16).all(), "token dictionary too large for uint16"
tokens_np_uint16 = tokens_np.astype(np.uint16) # 转换为 uint16
return tokens_np_uint16
def write_datafile(filename, tokens_np):
np.save(filename, tokens_np) # token 数组保存为 .npy 文件
nprocs = max(1, os.cpu_count()//2) # 进程数
# 多线程池并行处理
with mp.Pool(nprocs) as pool:
shard_index = 0 # 当前分片索引
# 预分配缓冲区来保存当前分片的数据
all_tokens_np = np.empty((shard_size,), dtype=np.uint16)
token_count = 0 # 当前分片已收集 token 数
progress_bar = None
for tokens in pool.imap(tokenize, fw, chunksize=16):
if token_count + len(tokens) < shard_size:
# 当前分片有足够空间容纳新的 tokens,直接加入并更新进度条
all_tokens_np[token_count:token_count+len(tokens)] = tokens
token_count += len(tokens)
if progress_bar is None:
progress_bar = tqdm(total=shard_size, unit="tokens", desc=f"Shard {shard_index}")
progress_bar.update(len(tokens))
else:
# 当前分片空间不足,剩余空间加入并保存当前分片,开始新的分片
split = "val" if shard_index == 0 else "train" # 第一个分片为验证集其余为训练集
filename = os.path.join(DATA_CACHE_DIR, f"edufineweb_{split}_{shard_index:06d}")
remainder = shard_size - token_count
progress_bar.update(remainder)
all_tokens_np[token_count:token_count+remainder] = tokens[:remainder]
write_datafile(filename, all_tokens_np)
# 准备下一个分片
shard_index += 1
progress_bar = None
all_tokens_np[0:len(tokens)-remainder] = tokens[remainder:]
token_count = len(tokens)-remainder
# 如果有剩余tokens,处理完所有文档后,保存最后一个分片
if token_count != 0:
split = "val" if shard_index == 0 else "train"
filename = os.path.join(DATA_CACHE_DIR, f"edufineweb_{split}_{shard_index:06d}")
write_datafile(filename, all_tokens_np[:token_count])加载数据代码修改
import numpy as np
def load_tokens(filename):
npt = np.load(filename)
ptt = torch.tensor(npt, dtype=torch.long)
return ptt
class DataLoaderLite:
def __init__(self, B, T, process_rank, num_processes, split):
self.B = B
self.T = T
self.process_rank = process_rank
self.num_processes = num_processes
assert split in {'train', 'val'}
data_root = 'edu_fineweb10B'
shards = os.listdir(data_root)
shards = [s for s in shards if split in s]
shards = sorted(shards)
shards = [os.path.join(data_root, s) for s in shards]
self.shards = shards
assert len(shards) > 0, f"no shards found for split {split}"
if master_process:
print(f"found {len(shards)} shards for split {split}")
self.current_shard = 0
self.tokens = load_tokens(self.shards[self.current_shard])
self.current_position = self.B * self.T * self.process_rank
def next_batch(self):
B, T = self.B, self.T
buf = self.tokens[self.current_position : self.current_position+B*T+1]
x = (buf[:-1]).view(B, T)
y = (buf[1:]).view(B, T)
self.current_position += B*T*self.num_processes
if self.current_position + (B*T*self.num_processes + 1) > len(self.tokens):
self.current_shards = (self.current_shard + 1) % len(self.shards)
self.current_position = B * T * self.process_rank
return x, y
train_loader = DataLoaderLite(B=B, T=T, process_rank=ddp_rank, num_processes=ddp_world_size, split='train')
# 参数修改
warmup_steps = 715 # GPT3 论文中描述的预热步数
max_steps = 19073 # 每步处理 2**19 tokens, 希望处理 10B tokens, 所以有 10B / 2**19 = 19073 步验证集评估
- 验证泛化能力,每100步打印一次验证集损失,确保未过拟合
val_loader = DataLoaderLite(B=B, T=T, process_rank=ddp_rank, num_processes=ddp_world_size, split='val')
# DataLoaderLite 类中
# reset 函数
def reset(self):
self.current_shard = 0
self.tokens = load_tokens(self.shards[self.current_shard])
self.current_position = self.B * self.T * self.process_rank
# __init__ 最后一行
self.reset(self)
# 训练过程
for step in range(max_steps):
t0 = time.time()
last_step = (step == max_steps - 1)
# once in a while evaluate our validation loss
if step % 100 == 0 or last_step:
model.eval()
val_loader.reset()
with torch.no_grad():
val_loss_accum = 0.0
val_loss_steps = 20
for _ in range(val_loss_steps):
x, y = val_loader.next_batch()
x, y = x.to(device), y.to(device)
with torch.autocast(device_type=device_type, dtype=torch.bfloat16):
logits, loss = model(x, y)
loss = loss / val_loss_steps
val_loss_accum += loss.detach() # 20步累积梯度,计算平均,打印验证集损失
if ddp:
dist.all_reduce(val_loss_accum, op=dist.ReduceOp.AVG)
if master_process:
print(f"validation loss: {val_loss_accum.item():.4f}")
# 训练
model.train()
optimizer.zero_grad() ...
# 也可隔一段时间进行采样查看; 详见 https://github.com/karpathy/build-nanogpt/blob/master/train_gpt2.py保存检查点
if step > 0 and (step % 5000 == 0 or last_step):
# optionally write model checkpoints
checkpoint_path = os.path.join(log_dir, f"model_{step:05d}.pt")
checkpoint = {
'model': raw_model.state_dict(),
'config': raw_model.config,
'step': step,
'val_loss': val_loss_accum.item()
}
# you might also want to add optimizer.state_dict() and
# rng seeds etc., if you wanted to more exactly resume training
torch.save(checkpoint, checkpoint_path)目前为止,只涉及预训练步骤,若要对话则需要SFT来微调成聊天形式,将数据集替换为更加对话式的数据集
