自然语言处理
自然语言处理,Natural language processing (NLP) ,有监督学习
序列模型
文本是一种序列数据,一句话是由一个个按顺序排列的单词组成的
数据表示
$X^{(i)} = [x_1^{(i)}, x_2^{(i)}, \dots, x_{T_x^{(i)}}^{(i)}]$: 第 $i$ 个样本的输入序列,有 $T_x^{(i)}$ 个元素(单词/字符等)
$Y^{(i)} = [y_1^{(i)}, y_2^{(i)}, \dots, y_{T_y^{(i)}}^{(i)}]$:第 $i$ 个样本的输出序列
$T_x^{(i)}$表示第 i 个训练样例的序列长度,$X^{(i)}$表示 i 序列中第 t 个元素
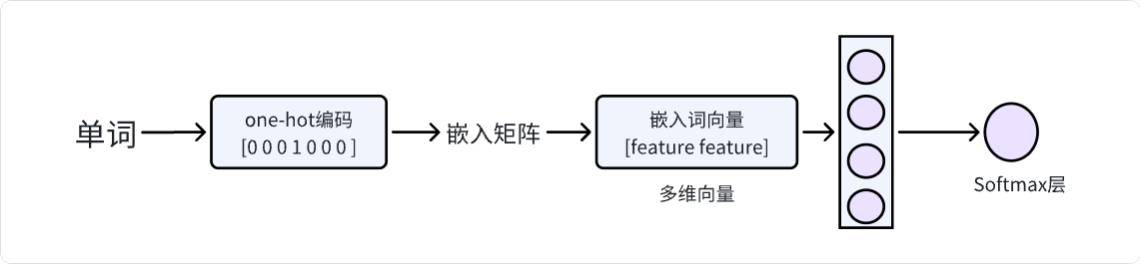
One-Hot 编码
存在单词字典列表,即每个单词对应一个等长向量列表,向量长度为词汇表大小 $|V|$
对应单词索引处为1其余为0
类别:RNN循环神经网络、LSTM长短期记忆网络、GRU门控循环单元、Transformer注意力机制核心
循环神经网络
- Recurrent Neural,处理一维序列化数据
- 关键思想:时间步之间共享权重,保留一个隐藏状态 $a^{<t>}$,表示前面序列的记忆
前向传播

初始隐藏状态:$a^{<0>}=\vec 0$
更新隐藏状态(Tanh, ReLU):$a^{<t>}=g(w_{aa}a^{<t-1>}+w_{ax}x^{<t>}+b_a)$
- 整合,将$W_{aa}$和$W_{ax}$矩阵左右联结表示为$W_a$,2 式转化为
- $a^{<t>}=g(W_a[a^{<t-1>}, x^{<t>}]+b_a)$,[ , ]中表示上下联结
- 输出预测(Sigmoid, SoftMax): $\hat y^{<t>}=g(w_{ya}a^{<t>}+b_y)$
基于时间反向传播
预测特定词是一个人名的概率是$\hat y$,使用逻辑回归损失
单个时间步损失:$L^{<t>}(\hat y^{<t>},y^{<t>})=-y^{<t>}\log \hat y^{<t>}-(1-y^{<t>})\log (1-\hat y^{<t>})$
总体损失函数:$L(\hat y, y)=\sum_{t=1}^{T_y}L^{<t>}(\hat y^{<t>},y^{<t>})$,$T_x$和$T_y$可能不同
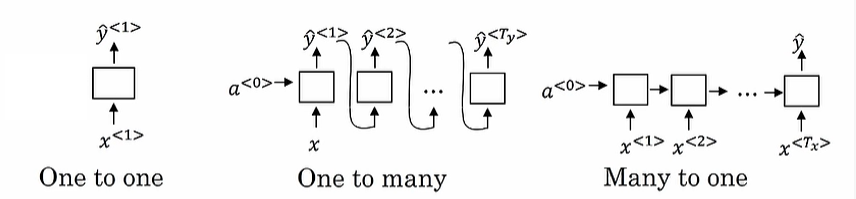
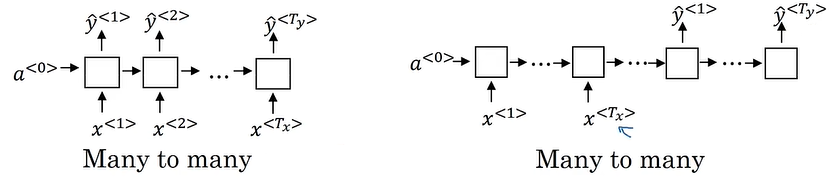
架构类型
一对一:图像分类等任务
一对多:图像描述
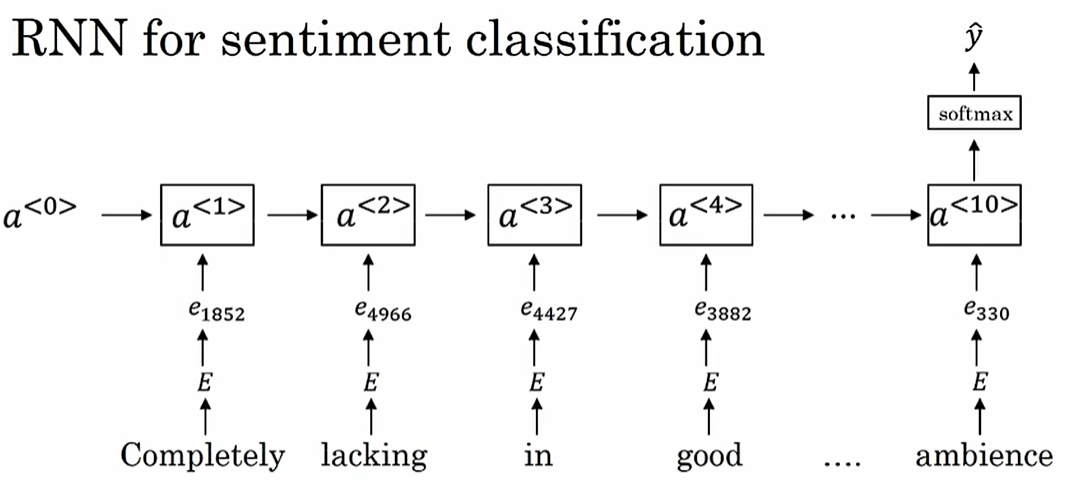
多对一:情感分类
多对多(对齐):命名实体识别(NER)
多对多(非对齐):机器翻译
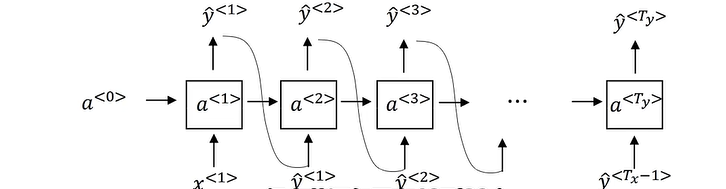
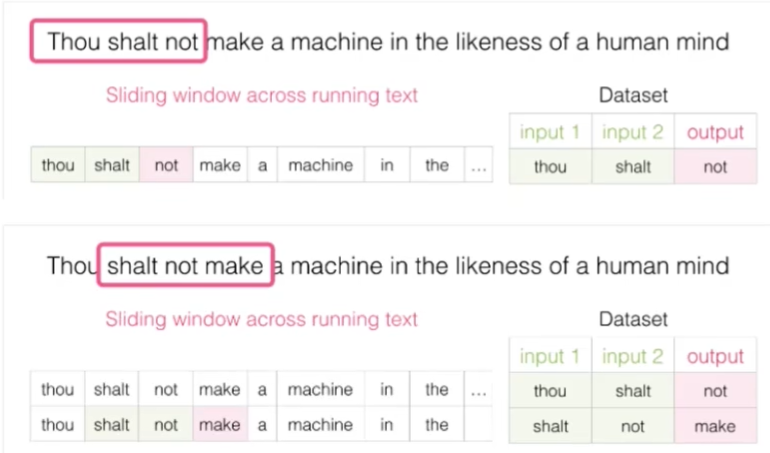
构建语言模型
目标:学习一个序列中下一个词的条件概率:$P(x^{<t>}|x^{<1>}, x^{<2>},\cdots, x^{<t-1>})$
数据处理
训练集为极大语料库(corpus),将数据句子标记化(tokenize),句子末尾加入<EOS>(End Of Sentence)标记,定位句子结尾,未知单词标记为<UNK>(unknown word)标记,$\hat y$ 对应于已知条件概率P(__|已知)
损失函数:对于每个时间步,$L(\hat y^{<t>},y^{<t>})=-\sum_iy_i^{<t>}\log \hat y_i^{<t>}$,softmax损失函数
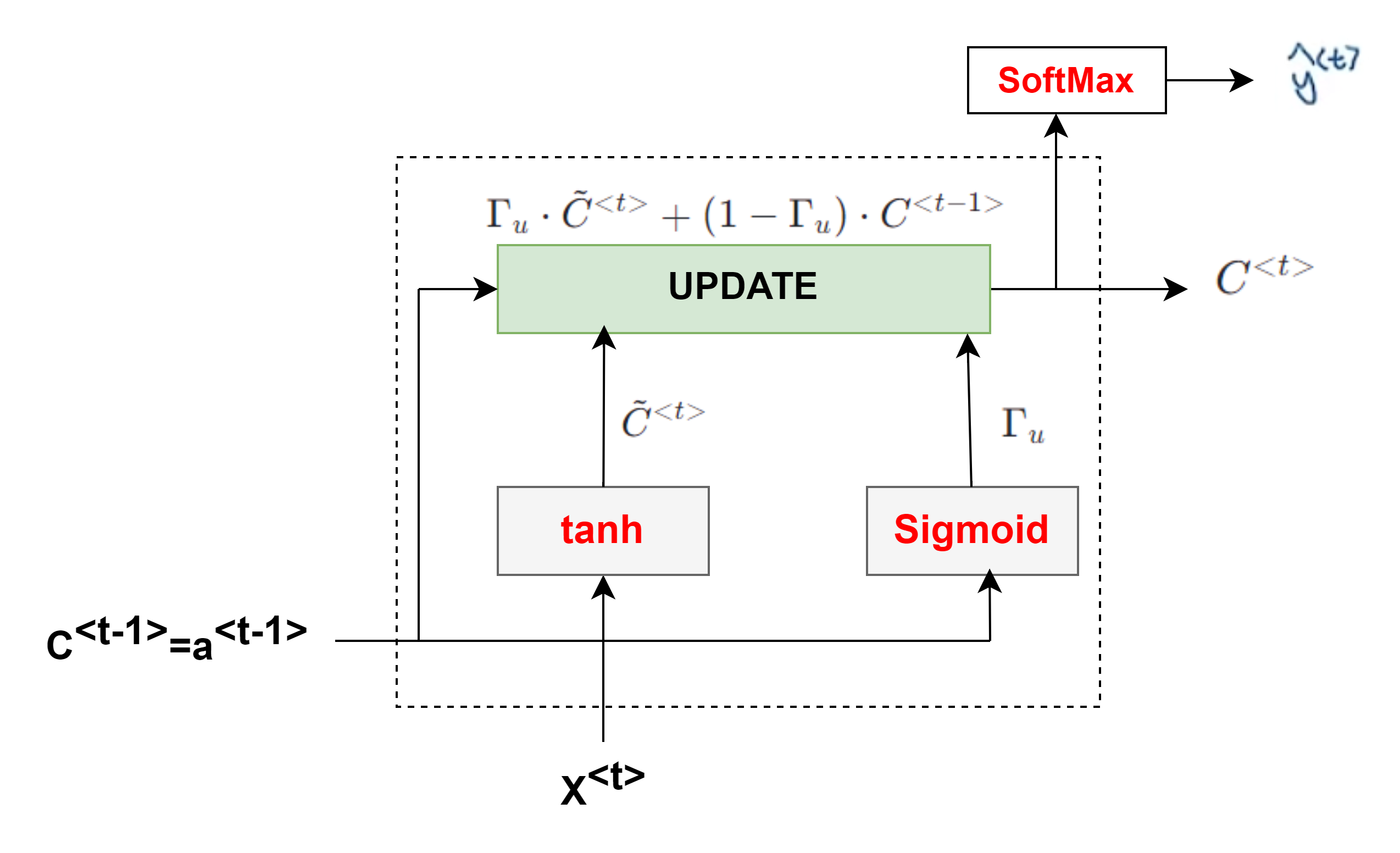
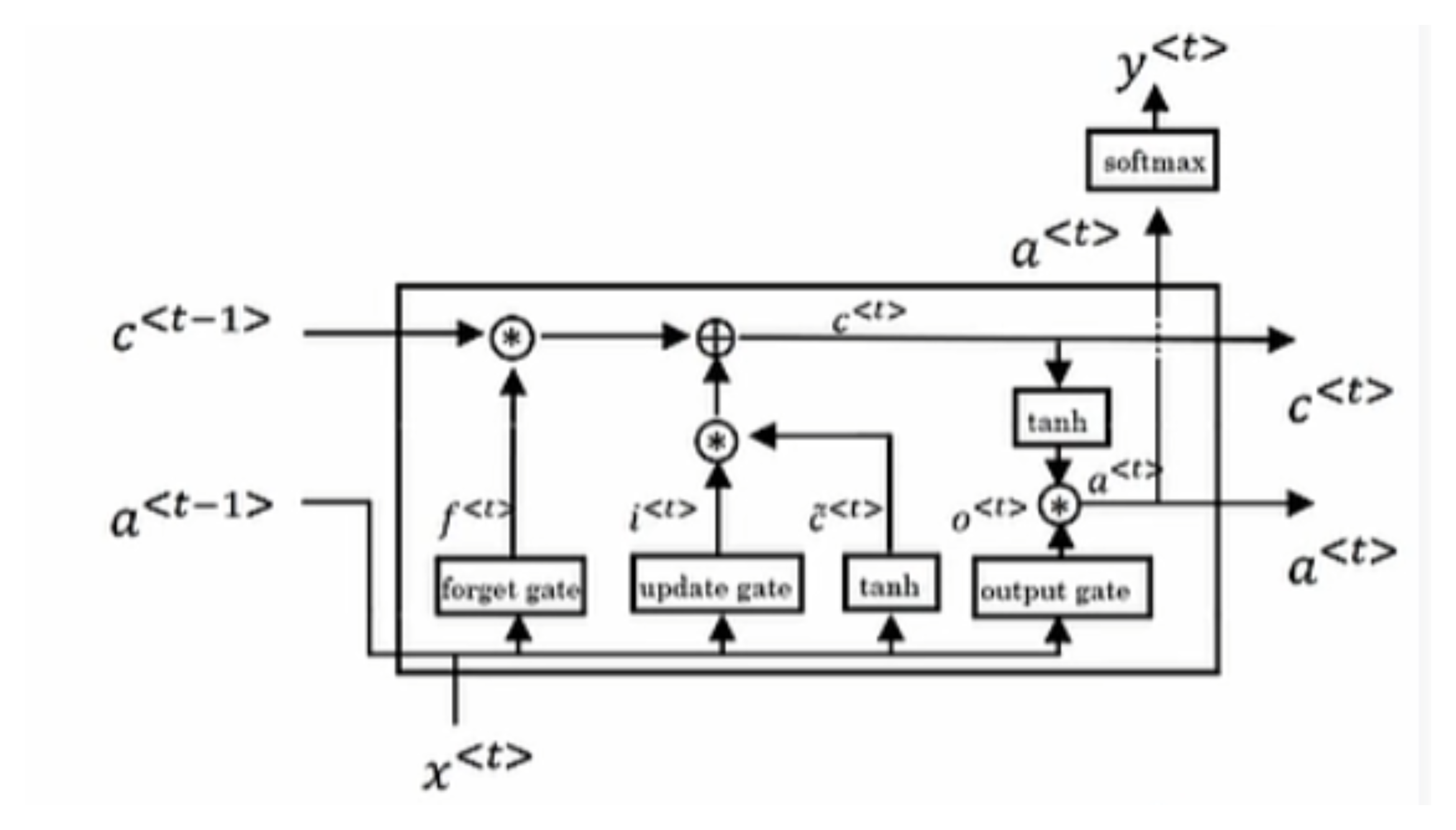
Gate Recurrent Unit(GRU)门控制单元
- 解决RNN梯度消失问题,引入了门机制来控制信息流动
- $C^{<t>}$记忆单元来存储记忆,如:需要记住cat是单数,使用was而不是were
- $\tilde C^{<t>}=\tanh (W_c[\Gamma_r\cdot C^{<t-1>},x^{<t>}]+b_c)$
- 门控值:更新门$\Gamma_u=\sigma(W_u[C^{<t-1>},x^{<t>}]+b_u)$,sigmoid使范围为0-1,为0表示不更新$C^{<t>}$,同样适用于相关性门$\Gamma_r$
- $C^{<t>}=\Gamma_u\cdot \tilde C^{<t>}+(1-\Gamma_u)\cdot C^{<t-1>}$ ,a和c相等
Long Short Term Memory Units(LSTM)长短期记忆单元
- $\tilde C^{<t>}=\tanh (W_c[a^{<t-1>},x^{<t>}]+b_c)$
- 更新门$\Gamma_u=\sigma(W_u[C^{<t-1>},x^{<t>}]+b_u)$,遗忘门$\Gamma_f=\sigma(W_f[C^{<t-1>},x^{<t>}]+b_f)$,输出门$\Gamma_o=\sigma(W_o[C^{<t-1>},x^{<t>}]+b_o)$
- 更新:$C^{<t>}=\Gamma_u\cdot \tilde C^{<t>}+\Gamma_f\cdot C^{<t-1>}$,$a^{<t>}=\Gamma_o\cdot C^{<t>}$,a和c不再相等
情感分类
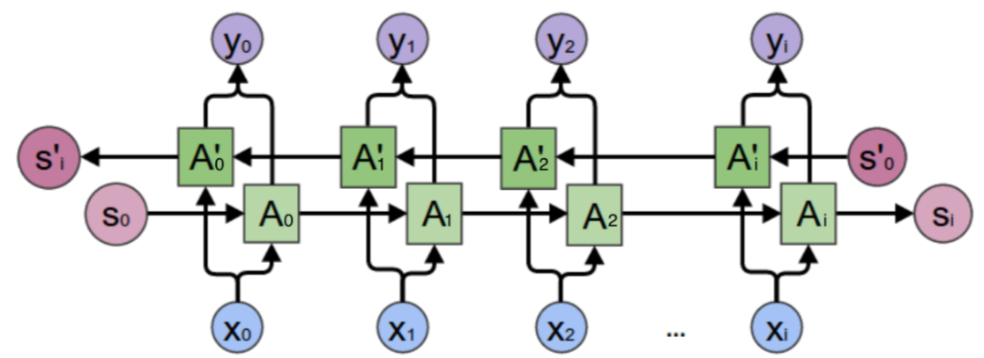
双向递归网络
- (bi-directional recurrent neural network, BRNNs)
- 解决单词不能单从前面得出是否是人名
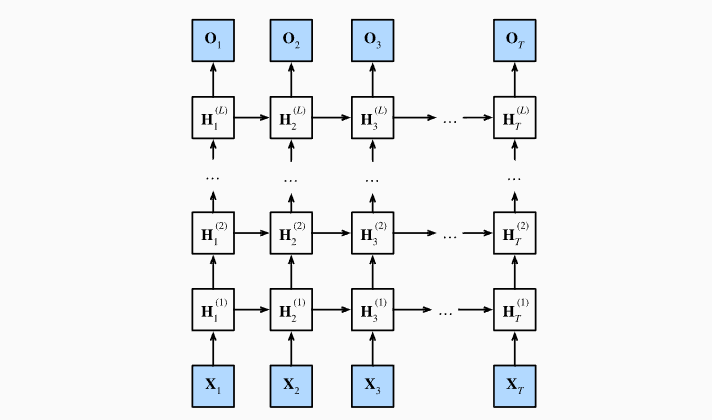
深度递归网络
- Deep RNNs
词嵌入模型
将文字或词语转换为一系列数字,通常是一个向量。词嵌入类似一个为每个词分配的数字列表,这些数字不随机,而是捕获了这个词的含义和它在文本中的上下文,使得语义上相似或相关的词在数字空间中比较接近
词向量表示
- one-hot编码两两单词相乘为0
- 需要描述一个物,需要综合多项指标(向量),向量可以用不同方法计算相似度,相似词在特征表达中比较相似
- 特征比如单词与性别(
-1~1)、年龄、是否为食物的指标值(0~1)
词向量相似性
1️⃣ 类比推理
$e_{king}-e_{man}+e_{woman} \approx e_{queen}$
2️⃣ 欧氏距离
衡量向量在几何空间的绝对距离:$d(u, v) = \sqrt{\sum_i(u_i-v_i)^2}$
3️⃣ 余弦相似度(相似函数)
- $\arg \max sim(e_w,e_{king}-e_{man}+e_{woman})$
- $sim(u,v)=\frac{u^Tv}{||u||_2\cdot||v||_2}$
- 实则求 u 和 v 之间的角$\phi$的余弦值,
0~180:1~-1
矩阵嵌入
使用单词矩阵与one-hot编码向量相乘获取对应单词的向量,实则一般在嵌入层中直接取对应列即可
词向量模型
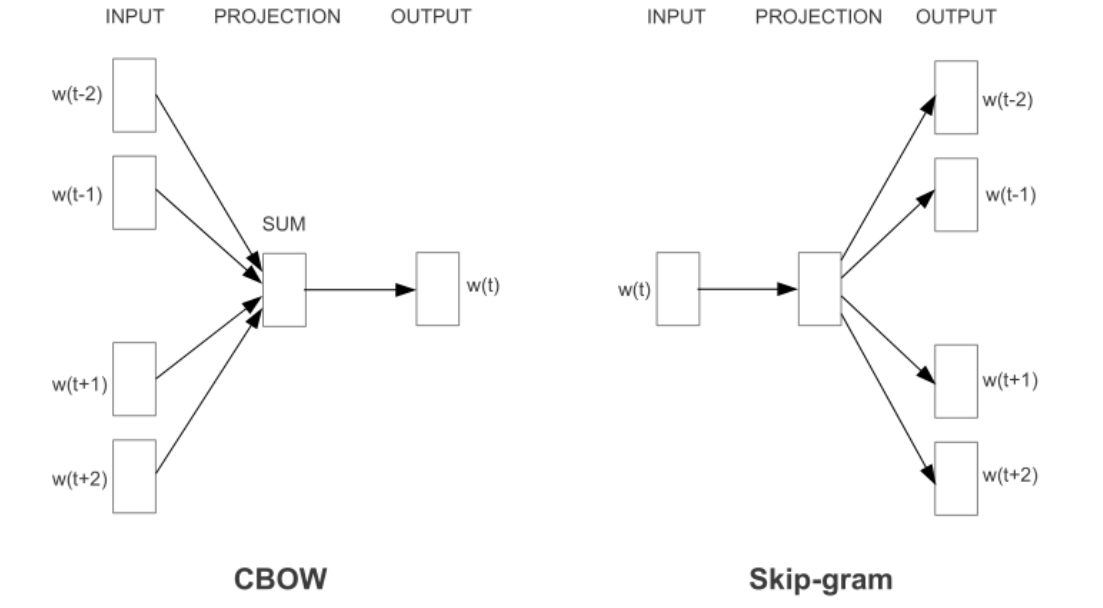
Word2Vec
Word2Vec 将单词嵌入空间中,通过上下文预测目标词或反向预测上下文
训练数据
两种结构:CBOW(上下文推词) 与 Skipgram(词推上下文)
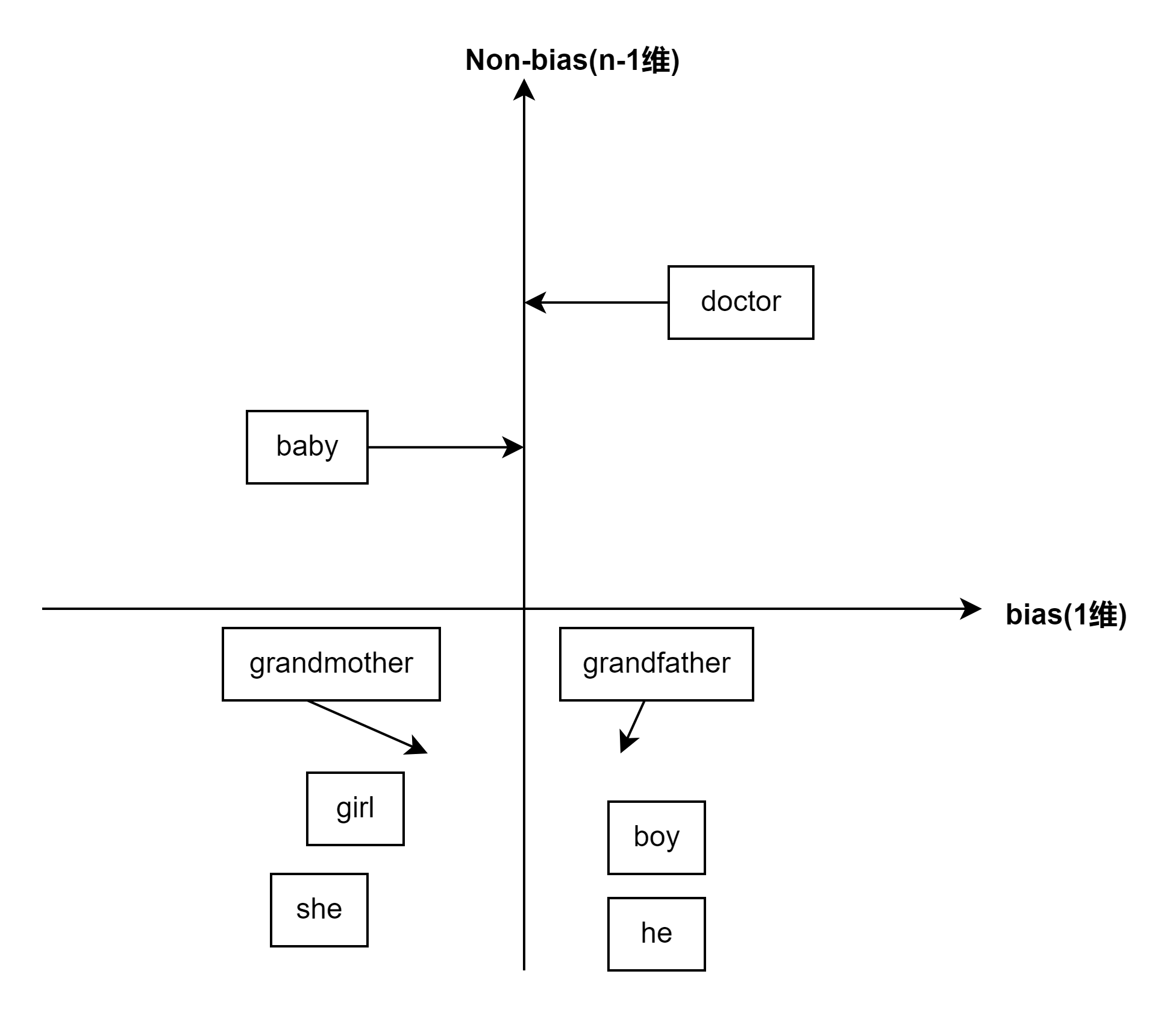
除偏(性别、种族偏差)
- 识别需要消除的偏差方向,使用$e_{he}-e_{she}$等多组的平均值获取坐标轴
- 中立化:未被定义的词通过映射到避开偏差
- 均匀化:移动相关性别的词使得距离坐标轴相等
Skip-gram
- 有监督学习
- 目标:给定上下文语境词 c,预测目标词 t ,$\theta_t$ 是关于 t 的参数,未包含偏置项
Softmax 概率函数:分母的运算代价极大
$p(t|c)=\frac{e^{\theta_t^Te_c}}{\sum_{j=1}^{10000}e^{\theta_j^Te_c}}$
负采样(Negative Sampling)
用 k 个词进行训练,其中:
- 1 个正样本(真实上下文词对)
- $k-1$ 个负样本(随机采样,不应出现在该上下文中)
使用 logistic 回归做二分类训练,使得正样本概率高、负样本概率低:
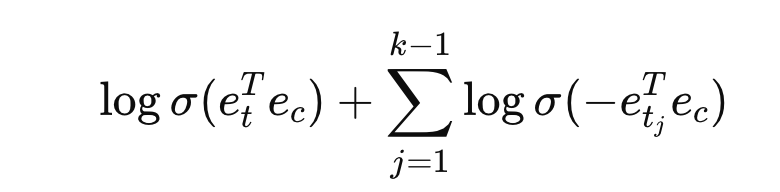
GloVe
Global Vectors for word representation,基于共现矩阵$X_{ij}$:词 i 和词 j 共同出现概率
$f(X_{ij})$是权重项,调整使得常见词权重不高,罕见词权重不低,X为0时f为0,采用"0log0=0"的规则
目标函数:带权重的平方损失
- $minimize,, \sum_{i=1}^{10000}\sum_{j=1}^{10000}f(X_{ij})(\theta_i^Te_j+b_i+b_j’-\log X_{ij})^2$
- 随机均匀初始化 $\theta,e$,梯度下降最小化目标函数
最终词向量:$e_w^{(final)}=\frac{e_w+\theta_w}{2}$
Seq2Seq模型
- (Sequence-to-sequence),机器翻译+语音识别
- 结构由两个 RNN(或LSTM/GRU)组成:
- 编码器 Encoder:将输入自然语言序列句子通过隐藏层编码成上下文向量(矩阵)
- 解码器 Decoder:通过隐藏层输出解码,逐步生成输出序列
- 先将语言经过编码器,然后经过解码器进行翻译,计算$P(y^{<1>}|x)$

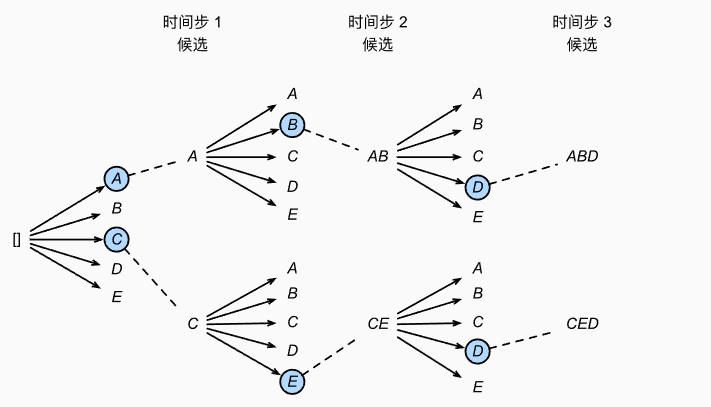
定向搜索
- Beam Search或集束搜索
- 参数B表示集束宽度,保留备选单词数,每次选择B个最高条件概率词元
- $\arg \max_y\frac{1}{T_y^{\alpha}}\sum_{t=1}^{T_y}\log P(y^{<t>}|x,y^{<1>},\cdots ,y^{<t-1>})$,$\alpha$=0.7取部分规范化
- $P(y^{<1>}\cdots y^{<T_y>}|x)=P(y^{<1>}|x)P(y^{<2>}|x,y^{<1>})\cdots P(y^{<T_y>}|x,y^{<1>},\cdots ,y^{<T_y-1>})$
Bleu指数
- 多个好结果下选择一个最好的看n元单词在参考翻译中出现概率
- $P_n=\frac{\sum_{n-grams\in \hat y}Count_{clips}(n-gram)}{\sum_{n-grams\in \hat y}Count(n-gram)}$再去各个n的平均值
- n个n个取参考翻译记录每n个单词的count,再在机器翻译中得出count_clip
- Bleu指数在句子长度小和极大时都很小
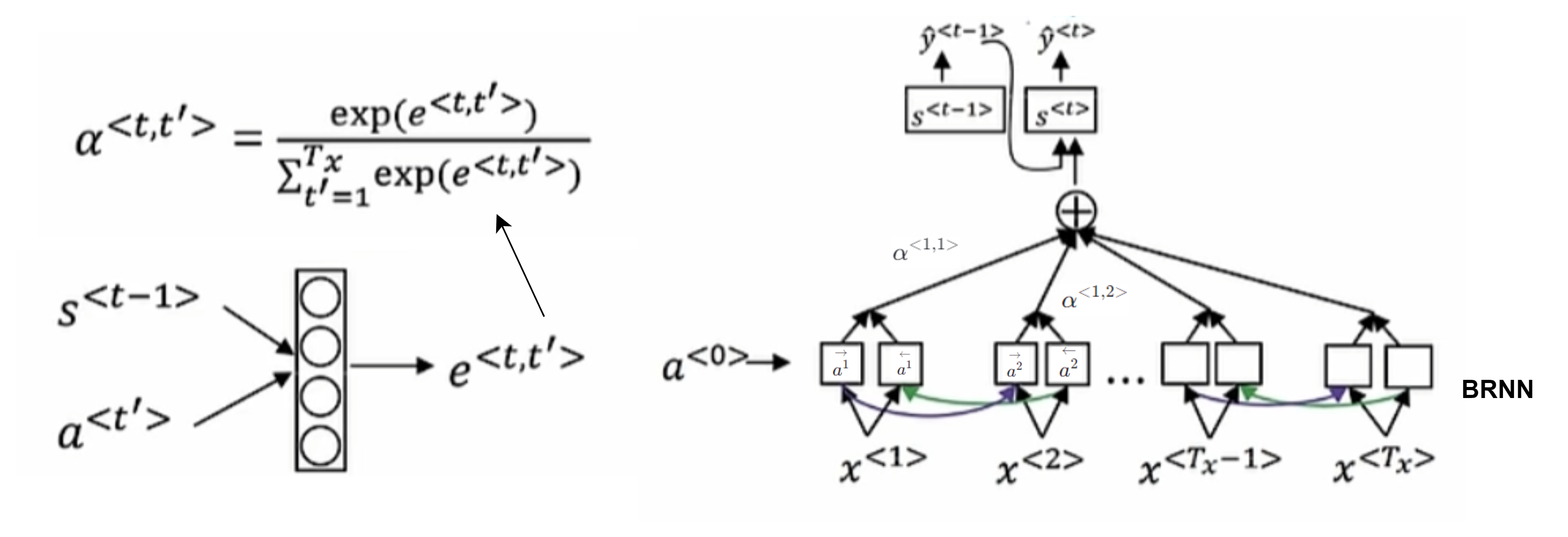
注意力模型
三个核心变量:查询值Query,键值Key,真值Value
(attention model),会生成多个注意力权重参数$\alpha$总和为1,将在某个词放入多少注意力,$\alpha^{<t, t’>}$ 表示生成 t 时需要对 t’ 花费的注意力是多少
{
"apple":10, // v or w = [0.5, -0.2, 0.3] 词向量
"banana":5,
"chair":2
}每个词具有词向量,表征语义,可用点积衡量相似性:$v\cdot w=\sum_iv_iw_i$
- 越大语义越相似,0则表示不相关,负值表示语义相反
查询Query为"fruit",对应词向量为q,将 q 与所有 key 的词向量点积获得相似度分数向量:$x=qK^T$,可计算出 Query 与每个键的相似度,结果仍为一列:[xx, xx, xx]
Softmax归一化:$softmax(x)=\frac{e^{x_i}}{\sum_je^{x_j}}$,输出为概率分布,和为1,将相似度转换为了注意力权重
将注意力分数和值向量对应乘积,获得一列:$attention(Q,K,V)=softmax(QK^T)V$
- 此处Q为矩阵,即多个查询的Query
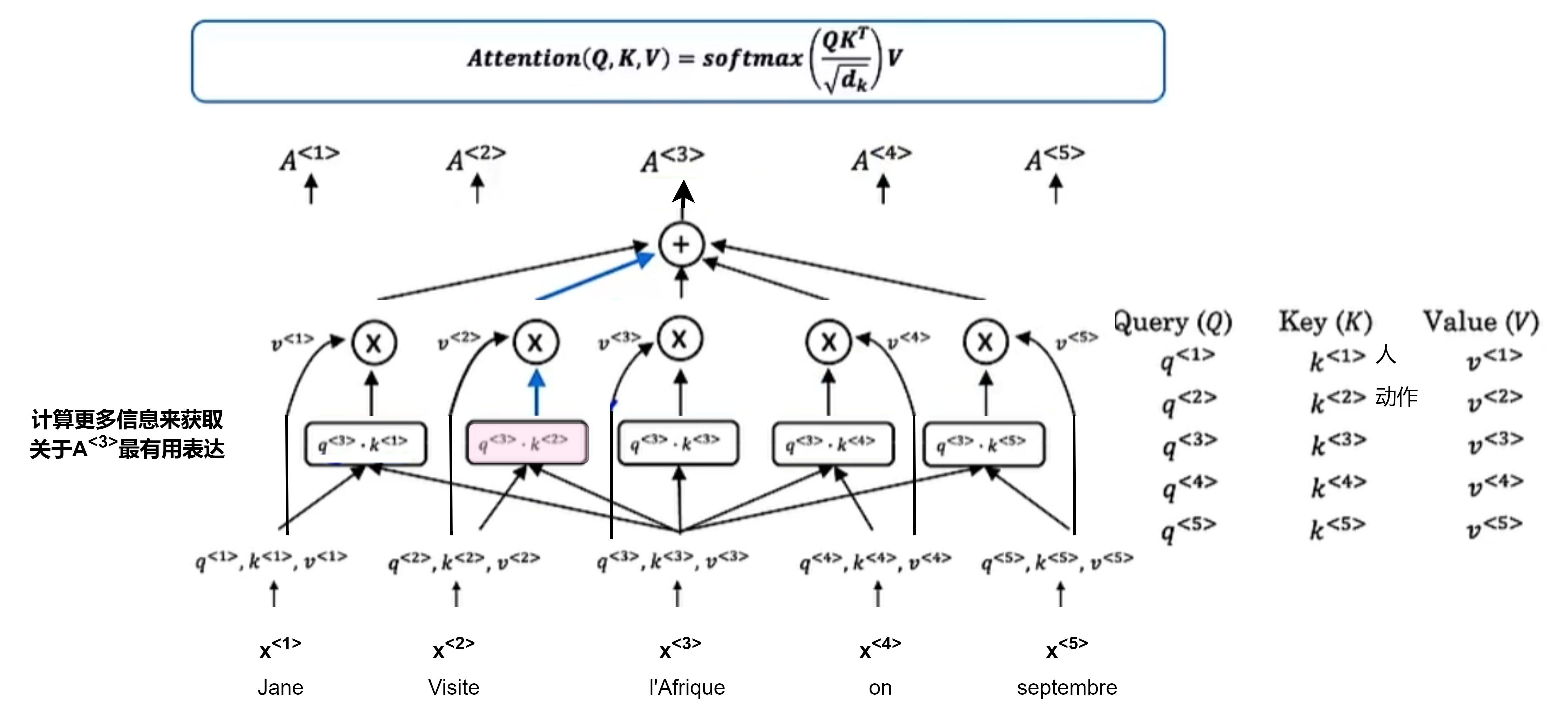
注意力机制:放缩Q和K维度,$attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$,输出注意力矩阵
Transformer
同一时间对一句话同时处理,注意力+卷积
自注意力机制:并行计算
计算本身序列中每个元素对其他元素的注意力分布,为每个单词计算出一个基于注意力的表达:$A(q,K,V)$,即$A^{<1>},A^{<2>},\cdots$

将每个单词与q(Query), K(Key), V(Value)关联,W为学习参数
- $q^{<i>}=W^Q\cdot x^{<i>}$
- $K^{<i>}=W^K\cdot x^{<i>}$
- $V^{<i>}=W^V\cdot x^{<i>}$
掩码自注意力机制:忽略一些被屏蔽的token,使得模型只使用历史信息而无法看到未来信息
- 可以达到并行预测效果
多头注意力机制:循环并行计算自注意力
通过不同矩阵参数集进行重复多次的自注意力计算,用于回答不同问题:when,where,who,how…
transformer架构
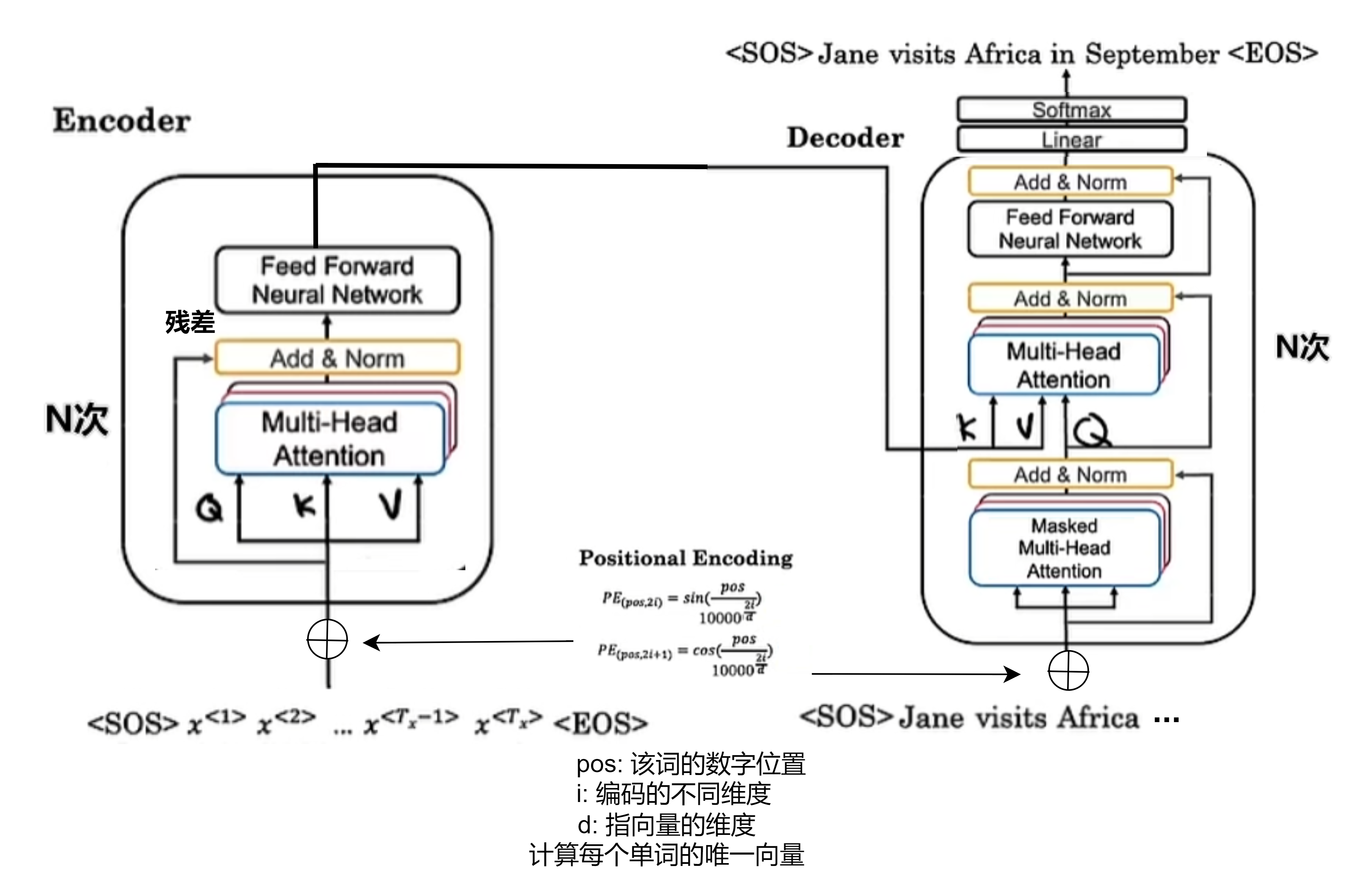
- 每个 Encoder/Decoder 由 6 个 Encoder/Decoder Layer 组成
