强化学习
概念
要素:$state\overset{policy}\longrightarrow action$
奖励函数
Reward Function,衡量智能体某个状态 s 下采取动作 a 后获得的即时反馈
$R(s,a)$,通过奖励好行为和惩罚坏行为使自动学习,
$(s_{start}, a, r(s_{start}, s_{change}))$
在初始状态$s_{start}$采取动作$a$,得到奖励$r(s_{start})$,状态转移为$s_{change}$
回报
return,从当前时刻到未来所有奖励总和,加权和,每一步奖励都乘以折扣因子
折扣因子(discount factor):$\gamma=0.9$,奖励随动作增加减少
$return=R_1 \cdot (\gamma) + R_2 \cdot (\gamma)^2 + \cdots + R_n\cdot (\gamma)^n$
策略函数
policy,策略 $\pi$ 为智能体在每个状态 $s$ 下选择动作 $a$ 的行为准则
- 确定性:$\pi(s)=a$,状态 $s$ 下一定选择动作 $a$
- 随机性:$\pi(a|s)=P(A=a|S=s)$,状态 $s$ 下选择动作 $a$ 的概率
目标:最大化回报
连续状态空间
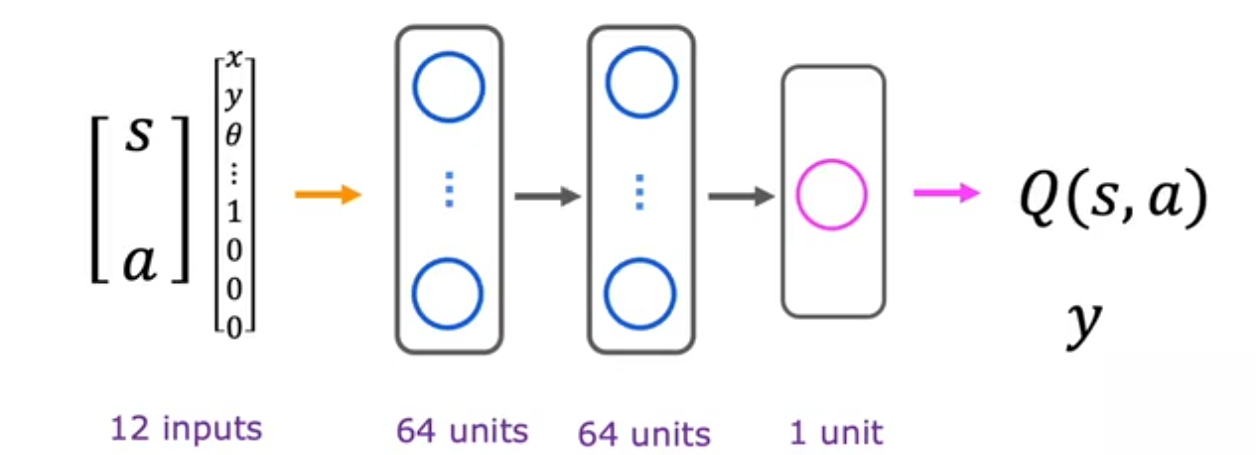
每个状态不是离散的,而是通过向量表示:$s=[x,y,\theta,x’,y’,\theta’]$可分别表示位置,方向,速度,角度等
该状态空间下,无法用表格表示所有状态,而是需要使用函数近似器:神经网络
ε-贪婪策略
强化学习中,智能体面临两难问题
1️⃣ > 利用exploitation:利用已有知识选择当前最好动作,最大化Q(s, a)
2️⃣ > 探索exploration:尝试其他动作,可能发现更好策略
ε = 0.05,逐渐减小 ε 使得前期多探索,后期稳定利用最优策略
0.95概率选择最大化 Q(s,a) 的动作 a:exploitation
0.05概率选择随机的动作 a :exploration
软更新
- 背景:深度 Q 网络(DQN)不稳定,若主网络每次更新都直接同步到目标网络,会导致训练不稳定
- 主网络(online network):$Q_{\theta}$,实时更新,选择动作
- 目标网络(target network):$Q_{\theta^{’}}$,生成目标值,更新慢,保持稳定
当使用小批量梯度下降时,更新 Q 的参数 w 及 b 时软更新,利于收敛:
$w=0.01w_{new}+0.99w$
$b=0.01b_{new}+0.99b$
$w_{new}$为主网络参数,$w$为目标网络参数,$\tau=0.01$为软更新系数
模型
MDP
马尔科夫决策过程:Markov Decision Process (MDP)
四元组:(S, A, P, R)
- S:状态空间
- A:动作空间
- P(s’|s, a):状态转移概率,从 s 采取动作 a 到状态 s’ 的概率
- R(s, a):奖励函数,从 s 采取 动作 a 得到的即时奖励
性质未来只取决于现在状态,与过去无关
状态-动作价值函数(Q-Function, Q(s, a))
Q函数表示在状态 s 下采取动作 a 后期望总回报
- 最优Q函数:Q*(s, a),从 s 开始,执行动作 a,按照最优策略执行后续动作,最终获得的最大期望回报
- 构建最优策略:$\pi^{*}(s)=\arg \max\limits_{a}Q^{*}(s,a)$
贝尔曼方程(Bellman Equation)
当前 Q 值 = 当前奖励 + 未来最大奖励的折扣期望
提供训练目标
1️⃣ 确定性环境:每个动作对应唯一下一个状态
- $Q(s,a)=R(s, a)+\gamma \max\limits_{a’}Q(s’,a’)=R_1+\gamma R_2 +\gamma^2 R_3 +\cdots= R_1+\gamma[R_2+\gamma R_3 +\cdots]$
2️⃣ 随机性环境:下一状态和奖励是概率分布
当出现随机情况,即下一个状态可能未实现,则更关注的是最大化多次运动下的期望回报
$Expected,,Return = Average(R_1+\gamma R_2+\gamma^2 R_3 +\cdots)=E[R_1+\gamma R_2+\gamma^2 R_3 +\cdots]$
$Q(s,a)=R(s)+\gamma E_{s^{’}}[\max\limits_{a’}Q(s’,a’)]$
MCTS
蒙特卡洛树搜索,The Monte Carlo Tree Search,给定一个游戏状态,选择最佳下一步
选择selection:选择最大化UCB值的结点,$UCB(S_i)=\overline{V_i}+c\sqrt{\frac{\log N}{n_i}}, c=2$
- $V_i$ 指该结点下平均价值,N探索次数,n当前结点探索次数
扩展node_expansion:创建一个或多个子节点
仿真Rollout:某一节点用随机策略进行游戏
Def Rollout(S_i): loop forever: if S_i is a terminal state: return value(S_i) A_i = random(available-actions(S_i)) S_i = simulate(A_i, S_i)反向传播back propagation:使用随机搜索结果更新搜索树,价值累加,探索次数加一
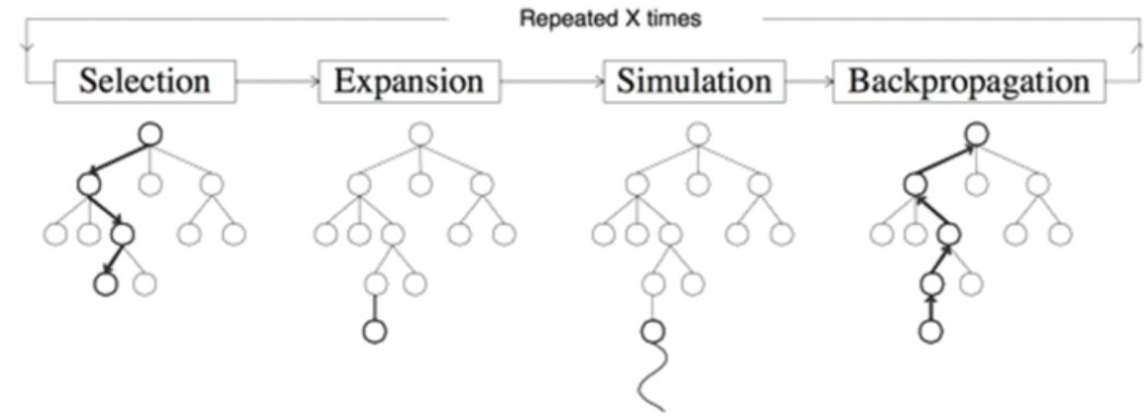
- 通过计算UCB最大值一直到叶结点,查看是否探索过,未探索过则仿真
- 探索过则枚举当前结点所有可能动作添加到树,扩展一个新结点
深度强化学习
- Deep Reinforcement Learning, DRL
学习状态值函数
- 使用神经网络去学习近似Q函数或策略函数,选择最大化 Q(s,a) 的动作 a
- 训练目标:最小化贝尔曼误差
$$Loss(\theta)=(Q_{\theta}(s,a) - [r + \gamma \max\limits_{a^{’}}Q_{\theta}-(s^{’},a^{’})])^2$$