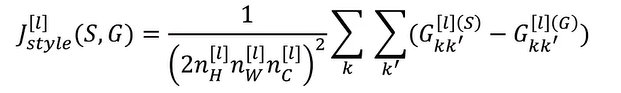计算机视觉
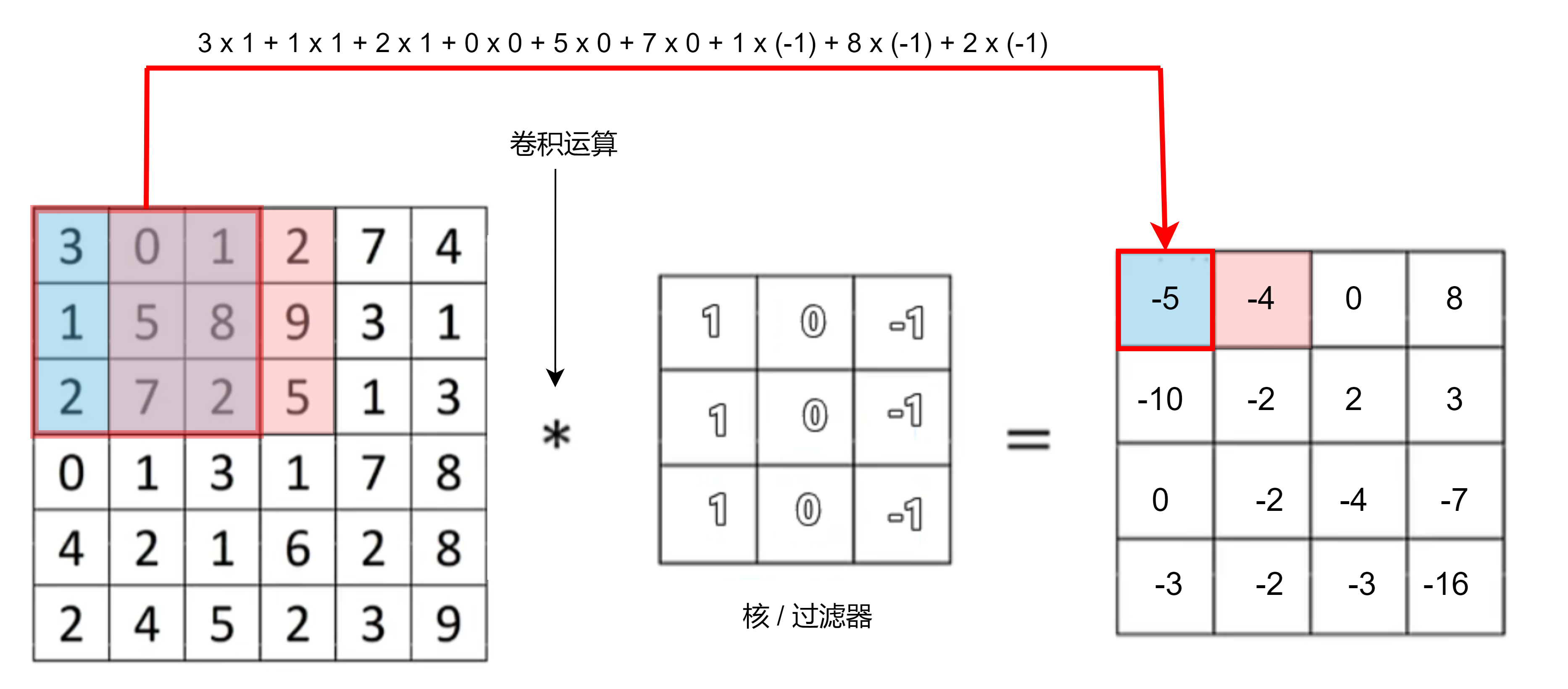
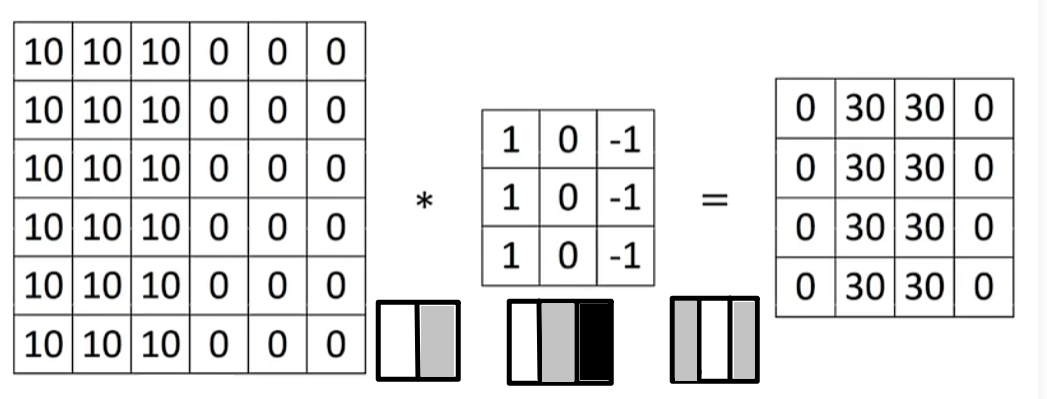
垂直边缘检测——灰度图
N x N * f x f = ( N - f + 1 ) * ( N - f + 1),f 基本为奇数
Sobel过滤器:1,2,1
Scharr过滤器:3,10,3
padding填充
- p=1时在矩阵外围填充一圈0
- (N + 2p) x (N + 2p) * f x f = ( N + 2p - f + 1 ) * ( N + 2p - f + 1)
Valid卷积:不进行填充;Same卷积:进行填充使卷积运算后矩阵大小保持不变
stride步长
- 过滤器每次计算后向上向下移动到新位置的长度均为步长,步长越大使得卷积结果矩阵大小越小,s=2时移动2格
- 输出:$( \lfloor\frac{N + 2p - f}{s} + 1 \rfloor) * ( \lfloor\frac{N + 2p - f}{s} + 1\rfloor)$
1x1卷积
2828192的输入,若要减少通道数,使用32个11192的滤波器卷积,输出282832大小的立方体
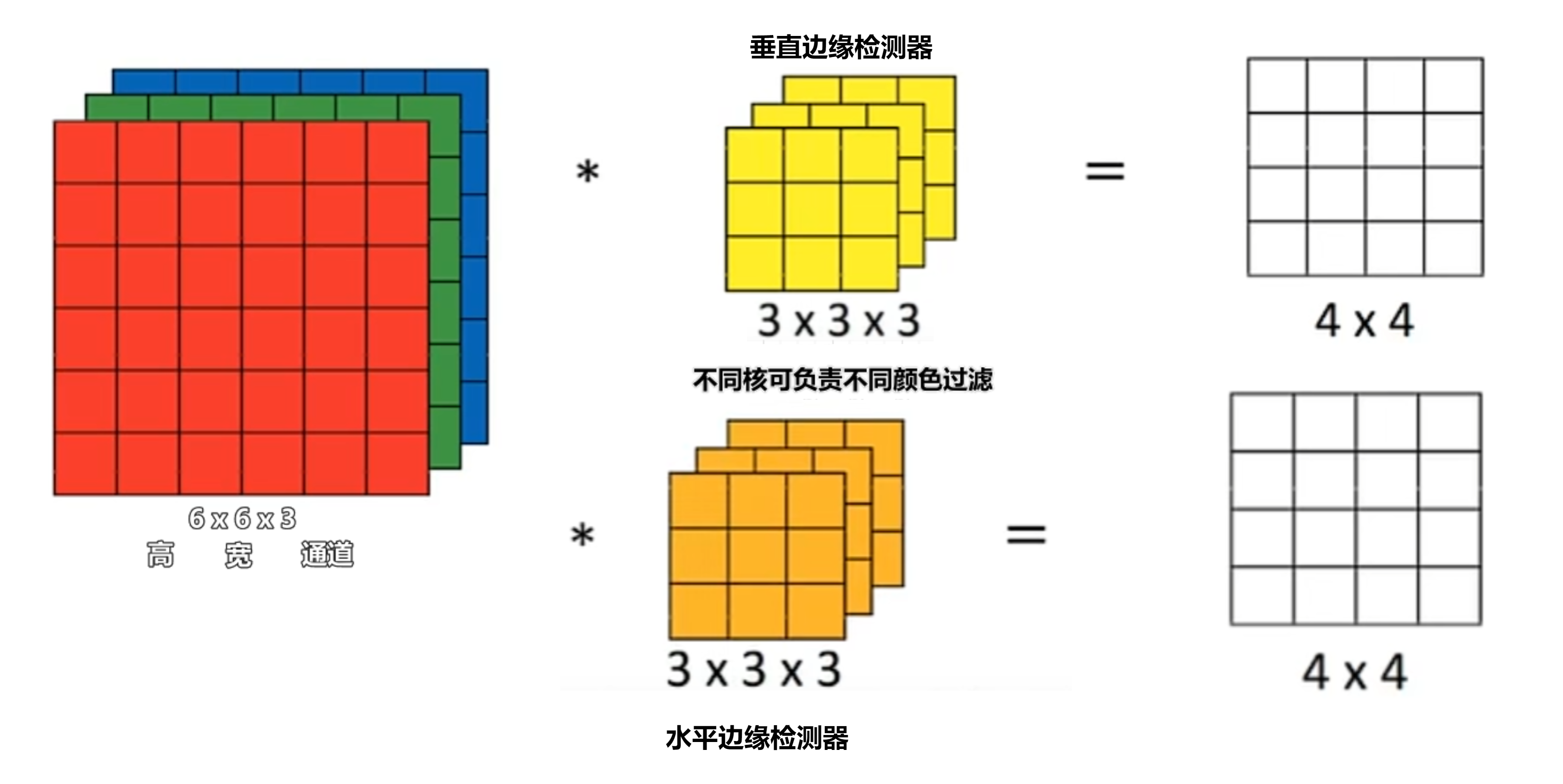
三维卷积
通道=深度
卷积神经网络
常用于图像数据处理
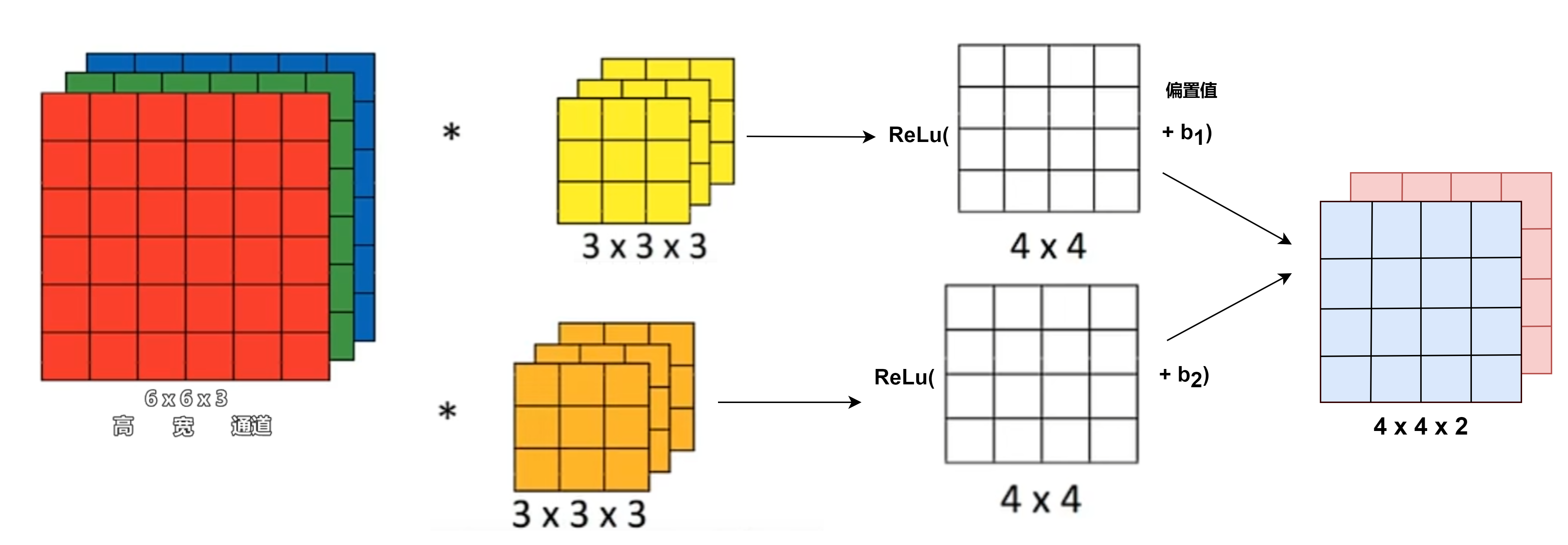
一层架构
2个过滤器即2个特征
多层架构:经过多个卷积核,最终展开输入Softmax单元或Logistic回归
参数
10个3x3x3过滤器,加入10个偏置值,一共10x(3x3x3+1)=280参数,不易过拟合
层类型
- 卷积层(Convolution, CONV)
- 池化层(Pooling, POOL):减少展示数量
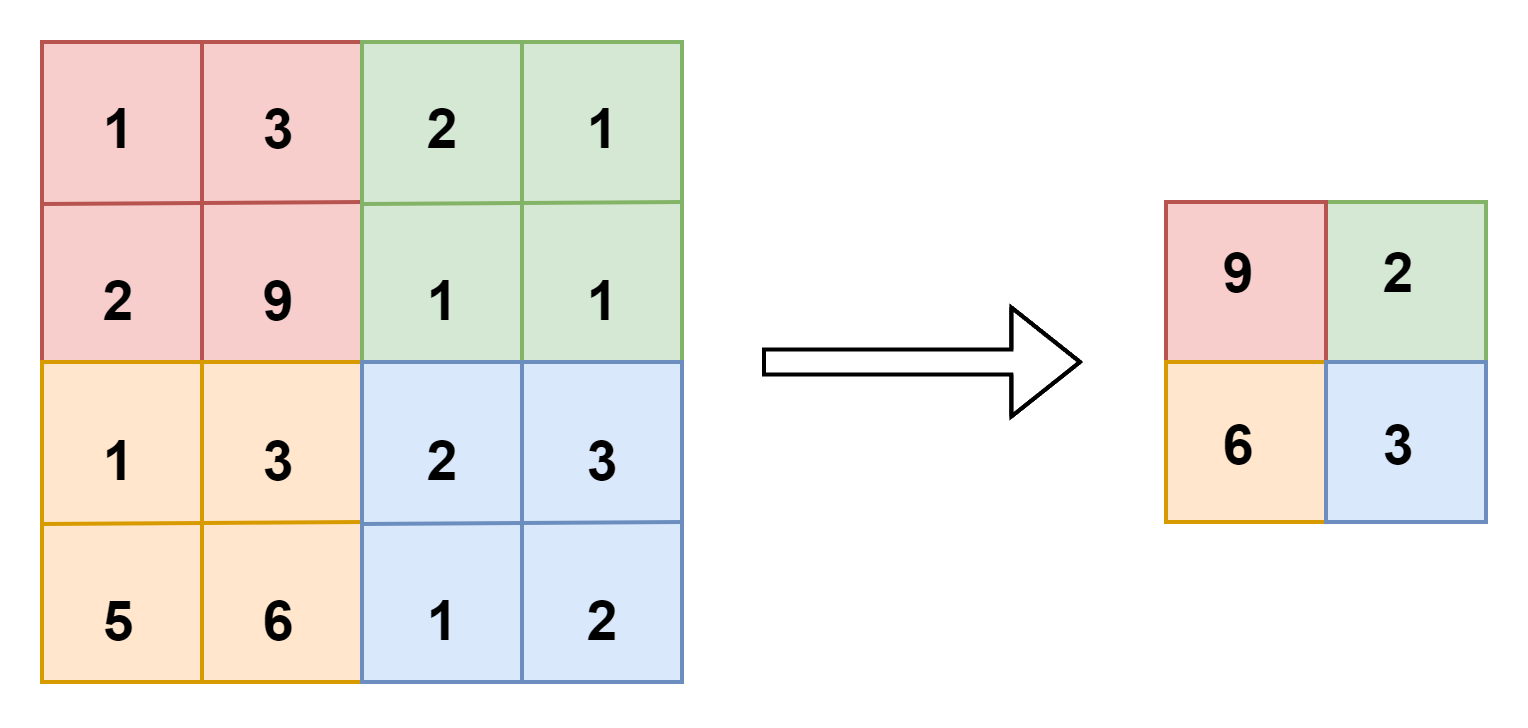
最大池化层(max pooling)
最大值采样:f=2,输出对应区域最大值,若在滤波器中任何地方检测到了特征,保留最大值
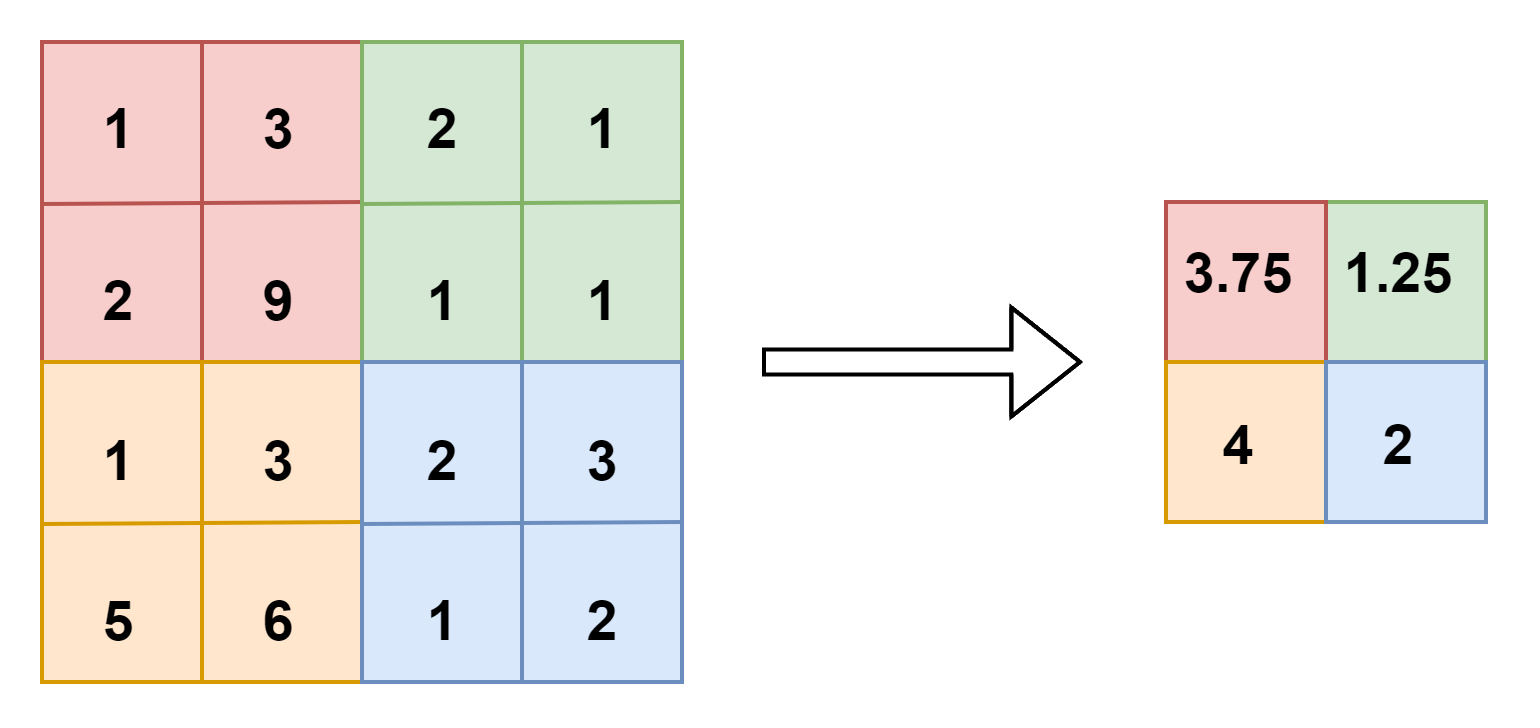
平均池化层(average pooling)
均值采样:f=2
池化层没有需要学习的参数,只需设置过滤器大小f,步长s
- 全连接层(Fully connected, FC)
经典架构
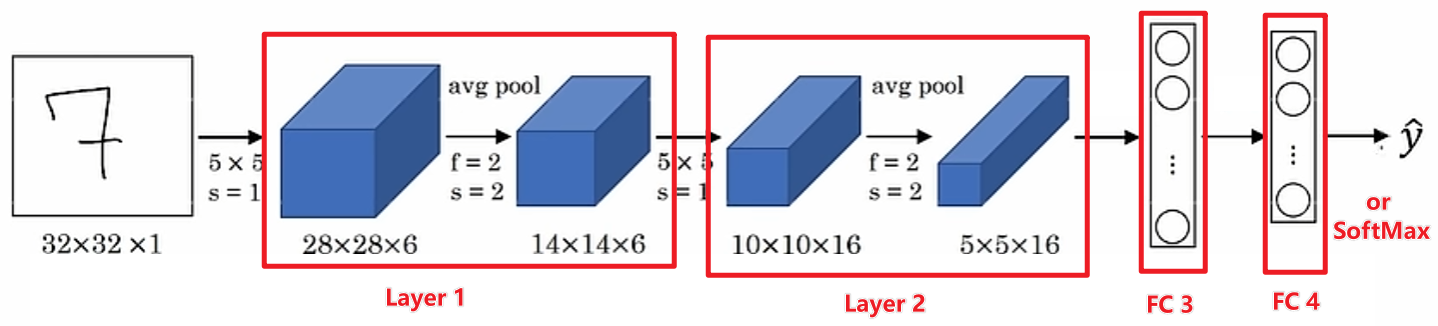
LeNet-5
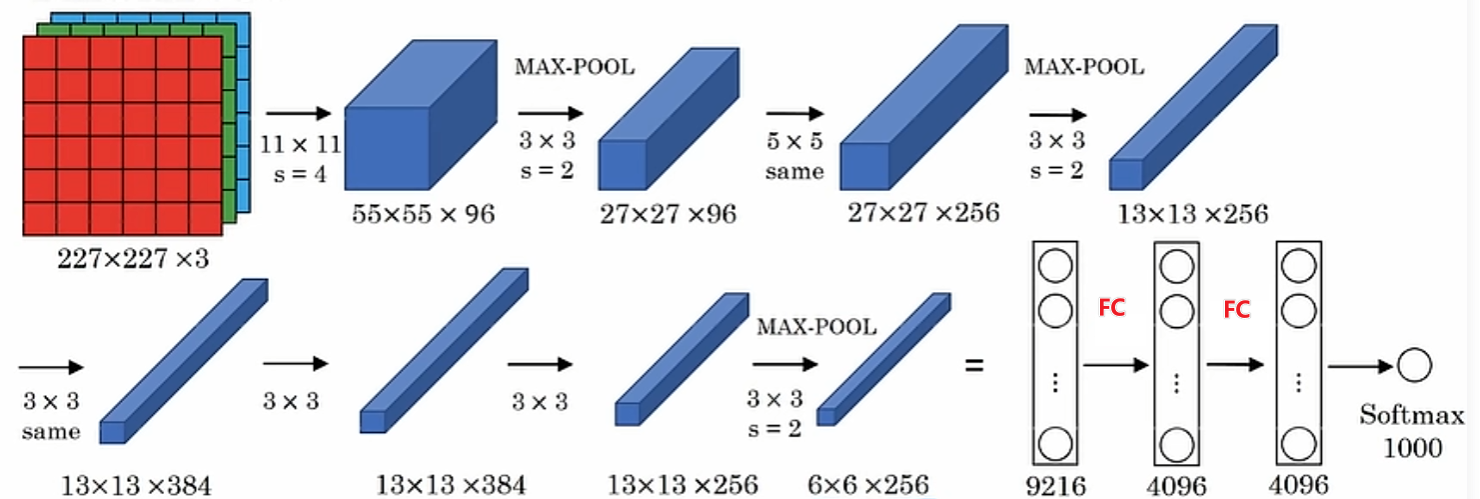
AlexNet
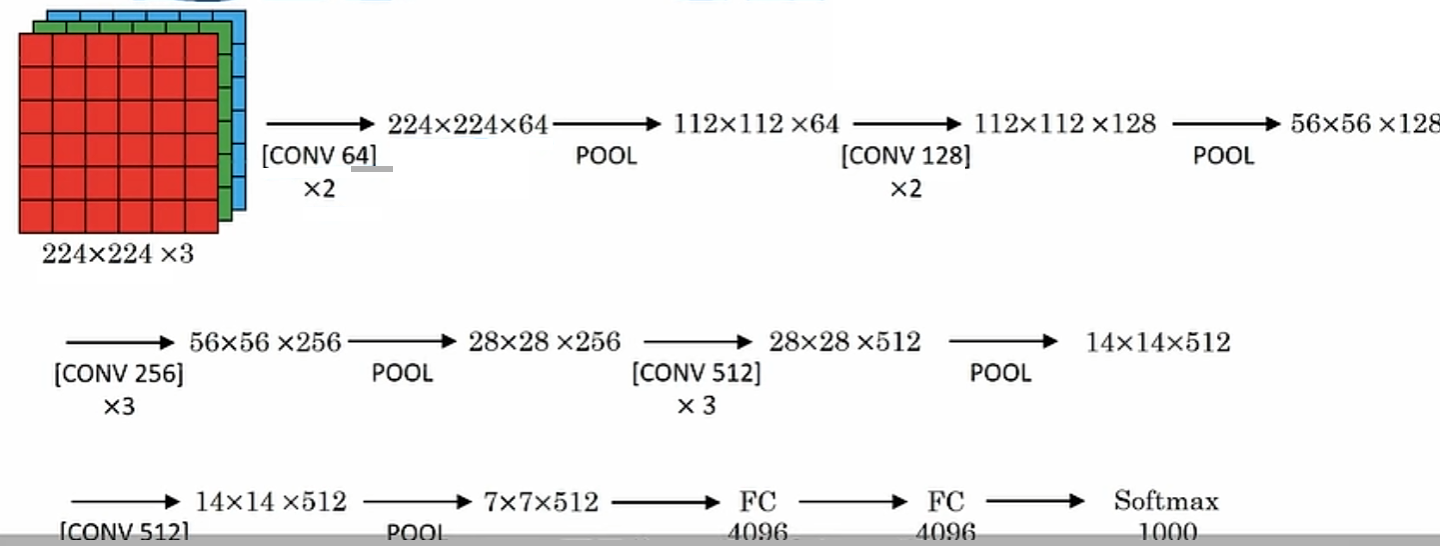
VGG-16
结构简单,更关注卷积层,有16层带权重的层
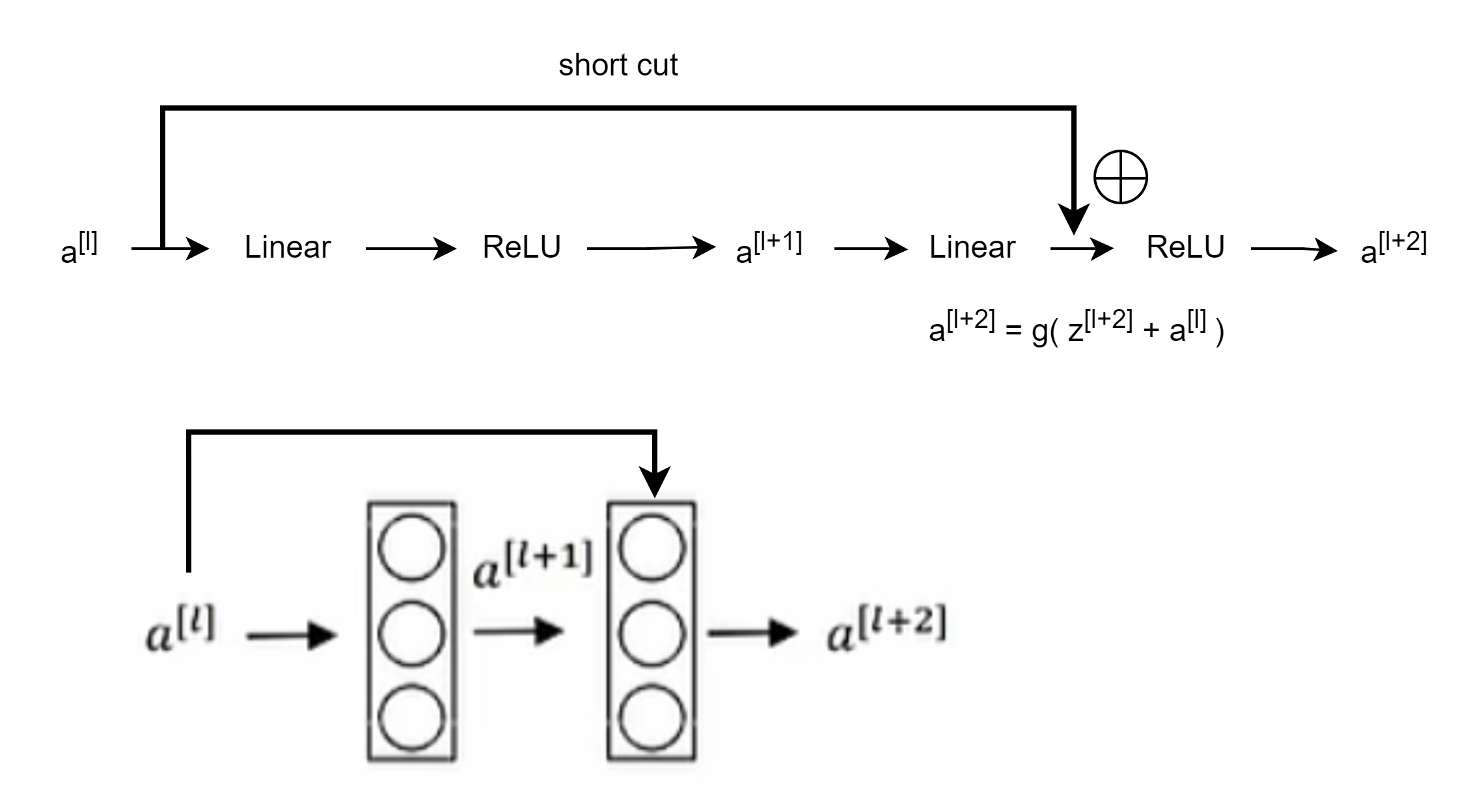
卷积残差网络
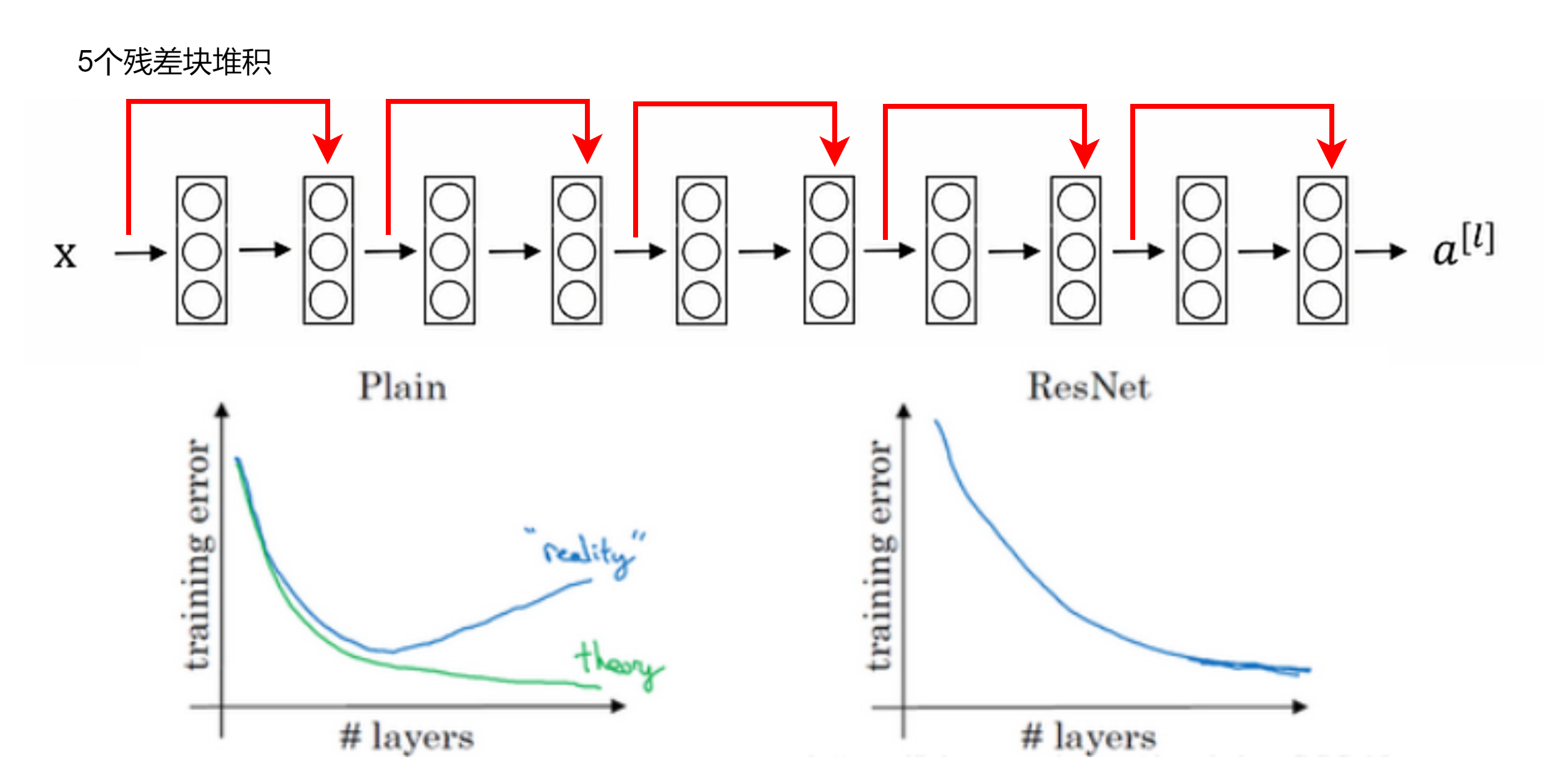
(conv residual network, ResNet),利用跳跃连接(skip connection),解决梯度爆炸和消失
残差神经网络ResNet
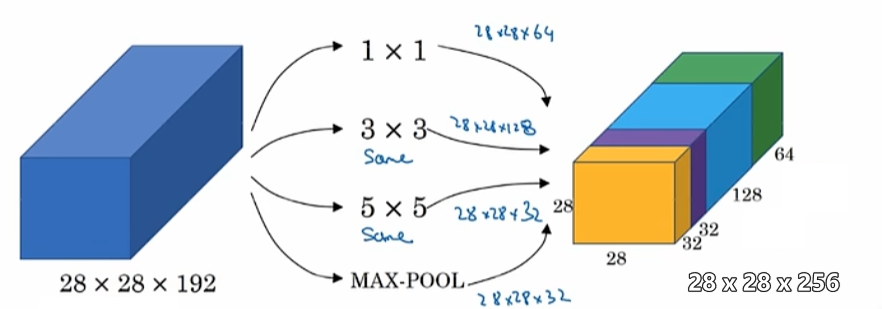
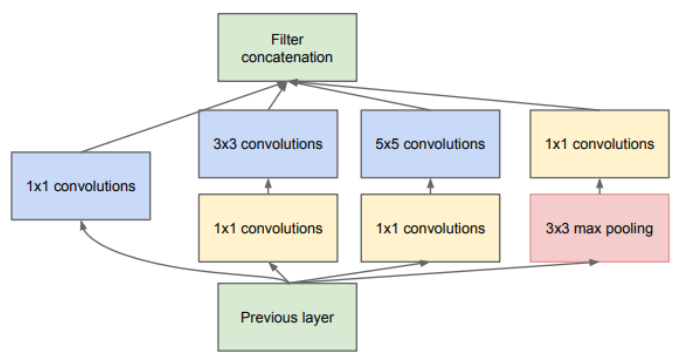
初始网络
(Inception network),做多次卷积并将结果合并
计算成本高,计算成本=卷积核的3个参数 x 卷积核所可移动的位置数 x 卷积核数量,若使用1x1卷积先减少通道数/维度化为瓶颈层(bottleneck layer)可大量减少计算成本
单模块
重复多次使用该单模块
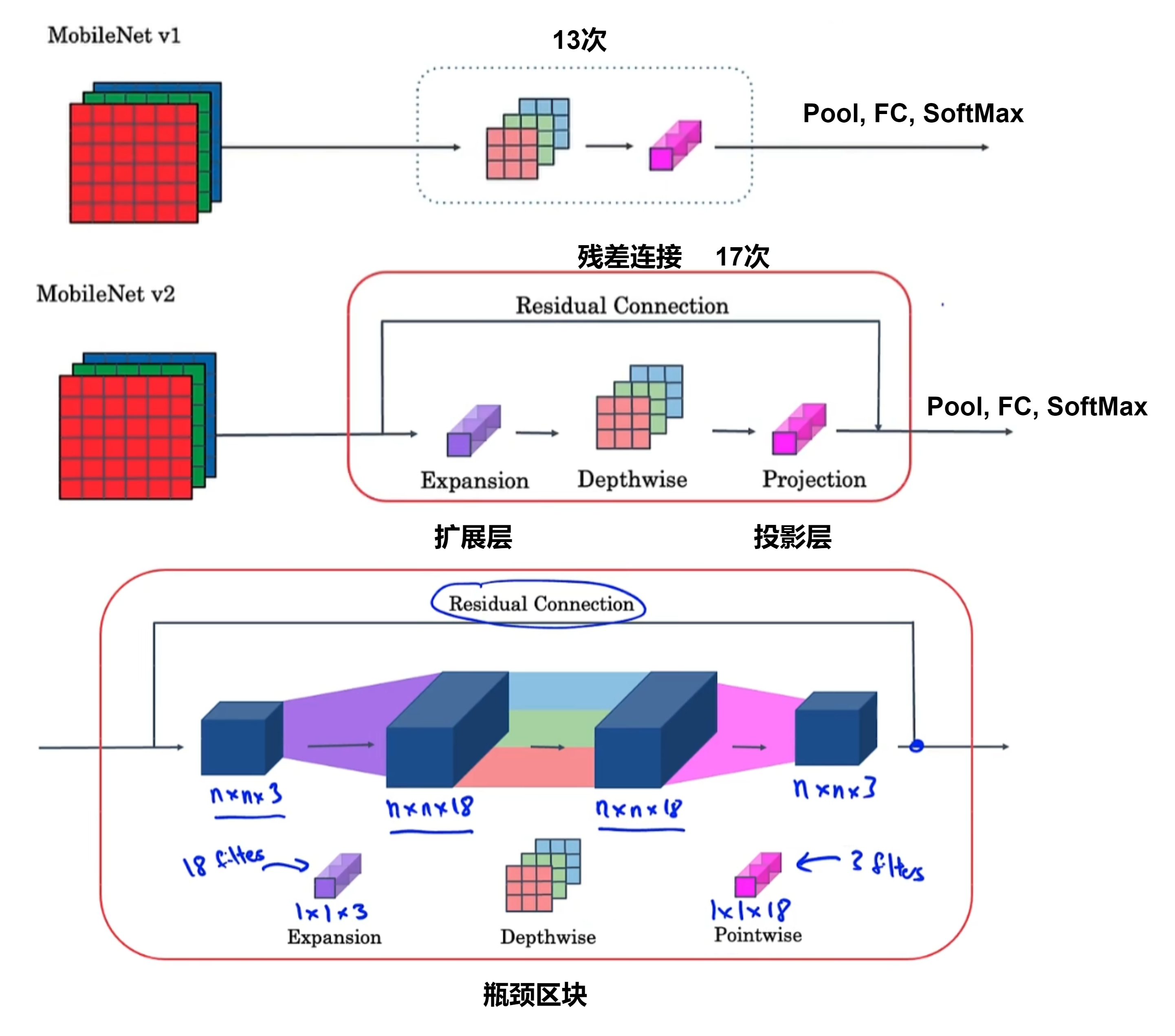
MobileNets
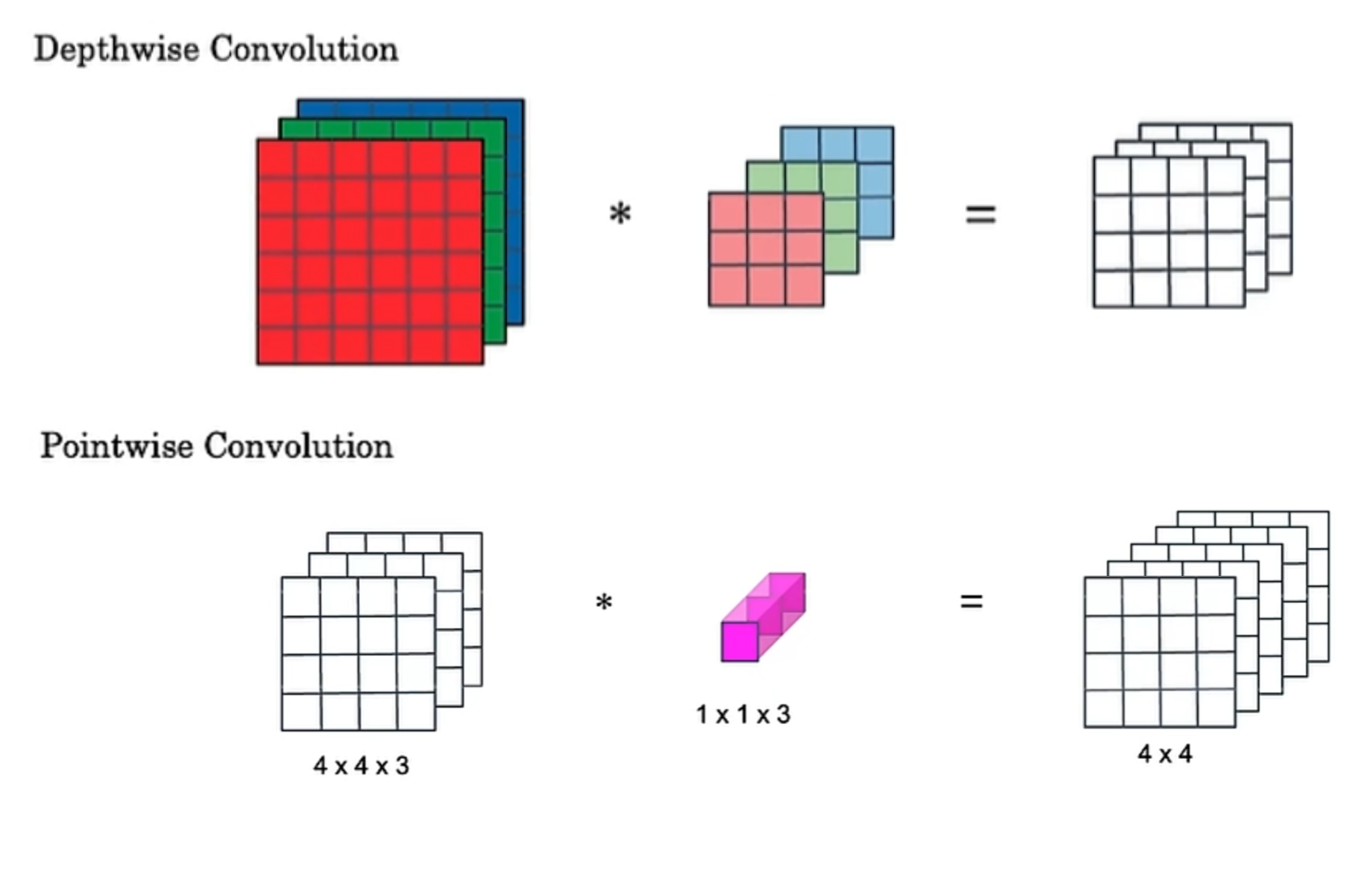
深度可分离卷积(depthwise-separable convolutions)
成本计算为:3x3x4x4x3 + 1x1x3x4x4x5 远小于一般卷积成本
架构
解决内存过小的问题,将输入值投射到较小的数据集
对象检测
目标定位
设置$b_x, b_y, b_h, b_w$:横坐标,纵坐标,高,宽,y 向量将包含是否有对象及概率$p_c$、$b_x, b_y, b_h, b_w$、是哪个对象$c_1,c_2,c_3$等
地标检测(Landmark detection)
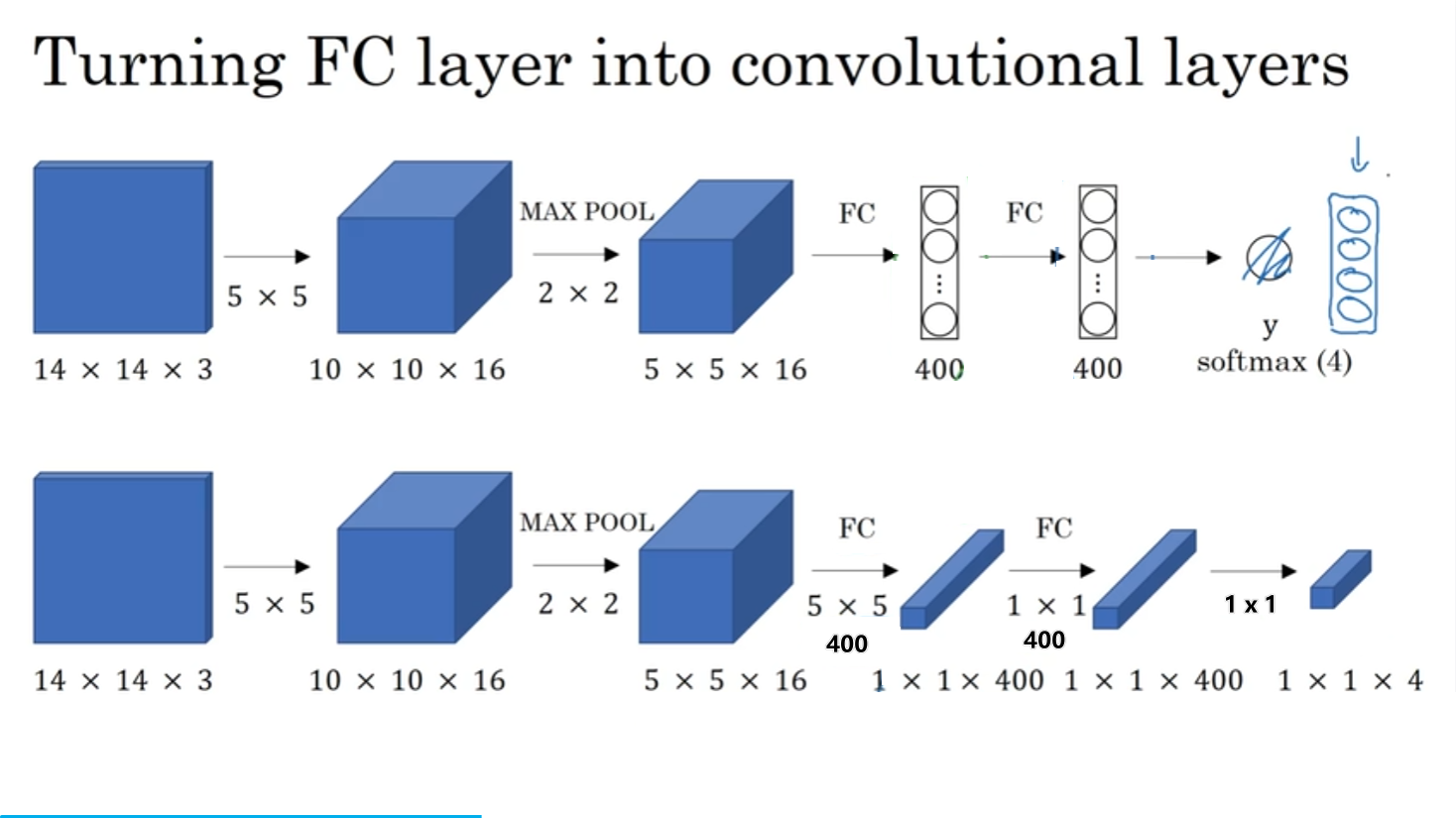
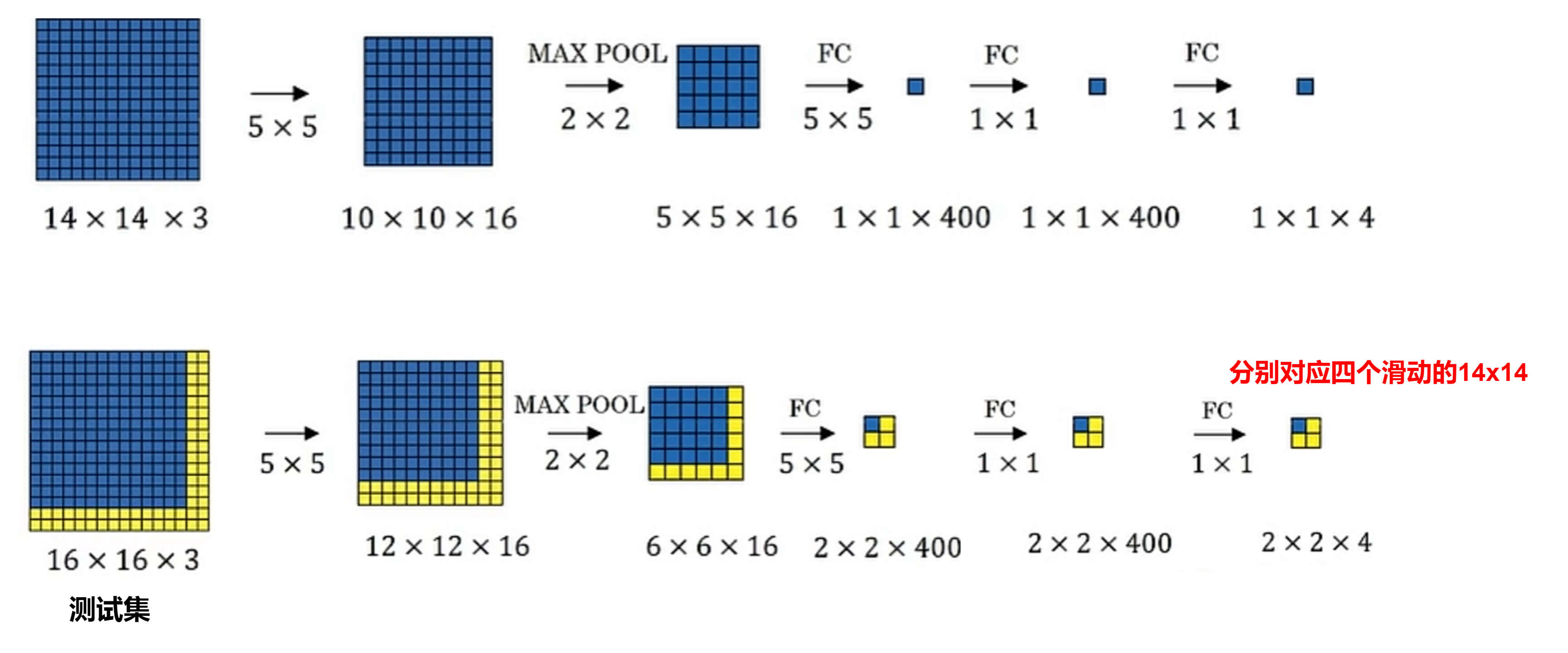
全连接层转换为卷积层
滑动窗口检测(sliding Windows Detection)
合并成一个前向传播运算,共享运算
YOLO算法
You only look once,边界框预测
$b_x, b_y, b_h, b_w$中:前两个只能小于1,后两个可大于1
交并比(Intersection over union)
将检测的框和真实的框交集部分大小比上并集大小,大于阈值0.5(可调)则正确,用于判断算法准确性
非极大值抑制
保证对每个对象只得到一个检测,选择最大可能性的边框,抑制其余邻近边框
锚框(anchor box)
一个网格单元检测多个目标,将输出 y 向量叠加一倍,维度翻倍,分别描述不同目标
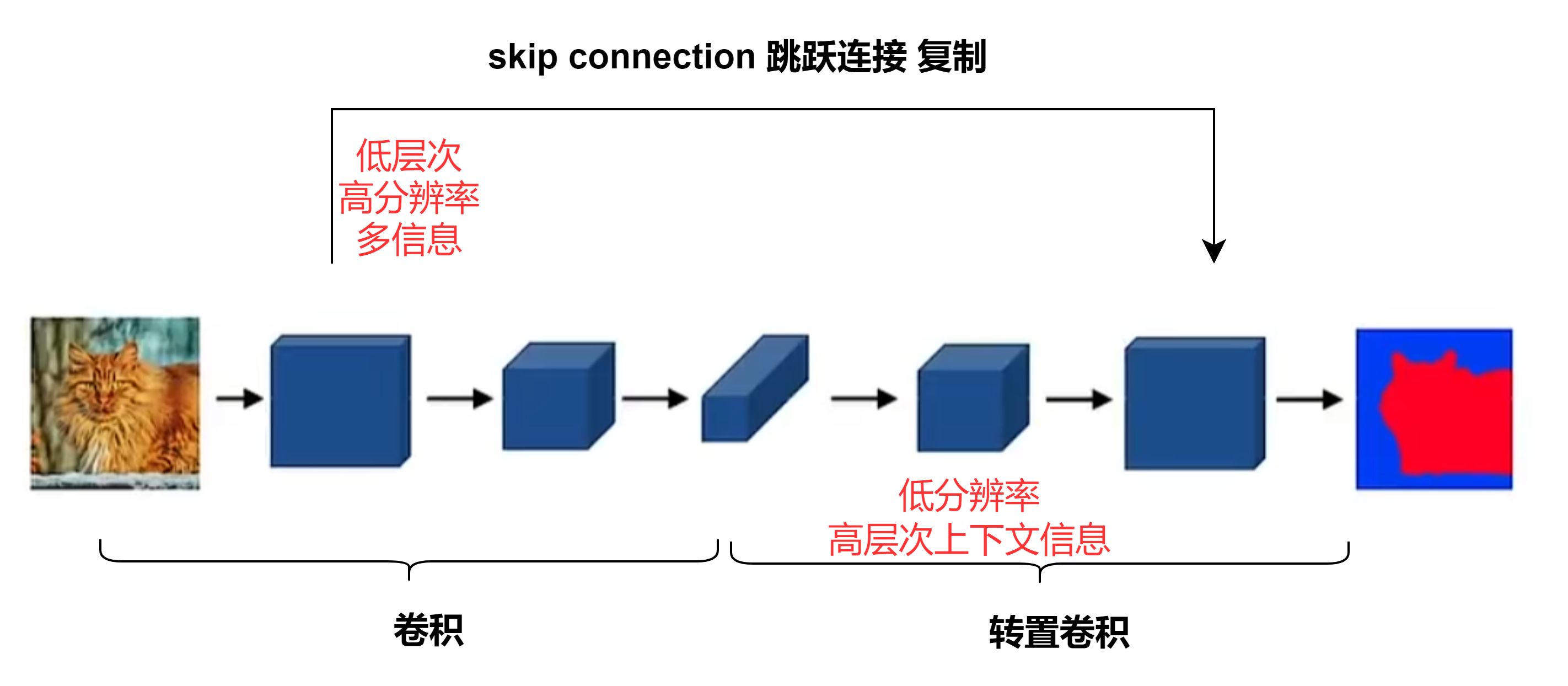
语义分割
Semantic Segmentation
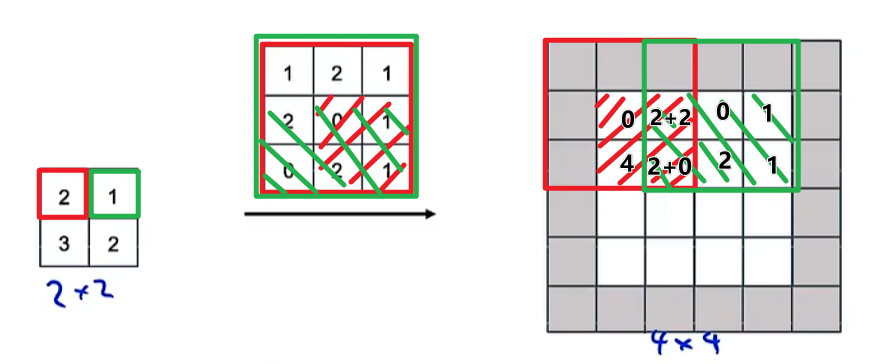
转置卷积(Transpose Convolution)
重叠部分叠加相加,padding为1,stride为2,灰色部分不填充,最终将2x2扩展为4x4
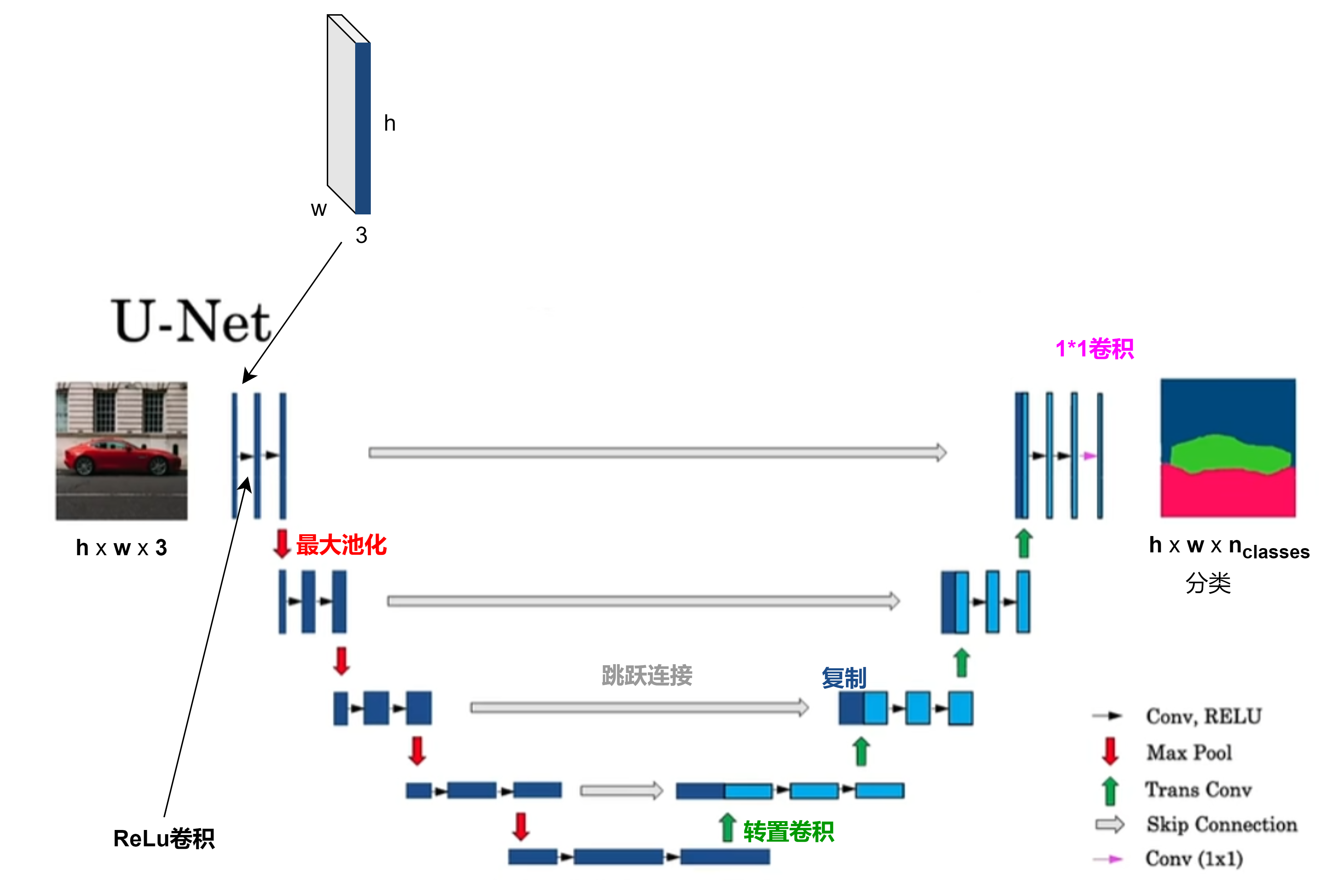
U-Net
人脸识别
One-shot learning,单样本学习:在只有一个样本情况下识别正确该人
相似方程:d(img1, img2) = 图像差异度 与 $\tau$ 比较
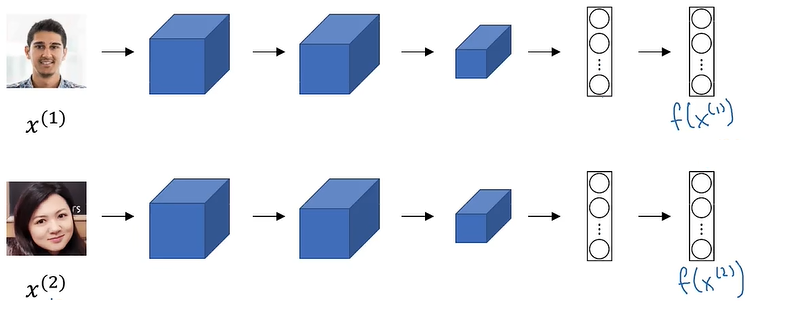
孪生网络(Siamese network)——用相同卷积网络对不同图片处理
$d(x^{(1)},x^{(2)})=||f(x^{(1)})-f(x^{(2)})||^2_2$同一个人值极小
三元组损失(Triplet loss)
存在A(Anchor), P(Positive), N(Negative)图片,$\alpha$表示margin,$||f(A)-f(P)||^2- ||f(A)-f(N)||^2+\alpha\le 0$
损失函数定义:$L(A,P,N)=\max(||f(A)-f(P)||^2- ||f(A)-f(N)||^2+\alpha,0)$
代价函数:$J=\sum_{i=1}^mL(A^{(i)},P^{(i)},N^{(i)})$
也可使用二分类逻辑回归,看两图片是否返回1或0分别表示相同或不同
神经风格迁移
图像:Content(C)和Style(S)形成Generated image(G)
代价函数:$J(G)=\alpha J_{Content}(C,G)+\beta J_{Style}(S,G)$
- 内容代价函数
$J_{Content}(C,G)=\frac{1}{2}||a^{[l][C]}-a^{[l][G]}||^2$,a 为激活因子,在 l 层
- 风格代价函数
风格矩阵/gram matrix:$a_{i,j,k}^{[l]}$表示高 i 宽 j 通道 k 的激活因子,$G^{[l]}:,,n_c^{[l]}\times n_c^{[l]}$记录每一对通道间的相关性
$G_{kk’}^{[l](S)}=\sum_{i=1}^{n_H^{[l]}}\sum_{j=1}^{n_W^{[l]}}a_{ijk}^{[l](S)}a_{ijk’}^{[l](S)},\quad\quad k=1,\cdots ,n_c^{[l]}$
$G_{kk’}^{[l](G)}=\sum_{i=1}^{n_H^{[l]}}\sum_{j=1}^{n_W^{[l]}}a_{ijk}^{[l](G)}a_{ijk’}^{[l](G)},\quad\quad k=1,\cdots ,n_c^{[l]}$
$J_{Style}^{[l]}(S,G)=\frac{1}{(\cdots)}||G^{[l][S]}-G^{[l][G]}||_F^2$
总风格代价函数
$J_{Style}(S,G)=\sum_l \lambda^{[l]}J_{Style}^{[l]}(S,G)$
更新参数:$G=G-\frac{\alpha}{2G}J(G)$